Revenons à des choses plus sérieuses.
J'ai donné plus haut une démonstration du fait que l'espérance du temps d'attente de retour à l'équilibre parfait pile-face était infini. Ce fait est intéressant par rapport au théorème central limite.
Ce théorème dit qu'étant donnée une suite de variables aléatoires
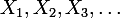
indépendantes et de même loi, telle que l'espérance
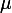
et l'écart-type
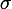
de cette loi existent et soient finis, alors la moyenne
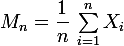[edit, je corrige une erreur de formulation] est proche pour
grand d'une variable gaussienne d'espérance
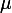
et d'écart type
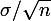
, précisément
)
converge en loi vers la loi normale standard.
Mézalor, que se passe-t-il avec notre temps d'attente du retour à l'équilibre, dont l'espérance est infinie ???? Ça vaut le coup de voir de plus près en faisant des simulations.
Pour cela, on écrit un code pour obtenir la moyenne sur
suites de tirages à pile ou face du temps d'attente du retour à l'équilibre pile-face. On voit rapidement qu'on ne s'en sort pas si on ne pose pas de limite à la longueur de la suite de tirages : on risque d'attendre très, très longtemps. Aussi dans le code ci-dessous écrit en python 2, on limite la longueur de la suite de tirages à 100 000. Si on atteint cette limite de 100 000 sans retour à l'équilibre, on retourne un temps d'attente de 100 000. Bien entendu, ça fait baisser les moyennes, mais il faut savoir faire des compromis !
- Code: Tout sélectionner
from random import *
def premier_retour() :
diff = 2*randrange(2)-1; nbtir=1
while (diff != 0 and nbtir < 100000) :
nbtir += 1
diff += 2*randrange(2)-1
return nbtir
def moyenne(n) :
tot = 0
for i in range(n) :
tot += premier_retour()
return tot/n
Et maintenant, on peut faire des histogrammes quand on prend des échantillons de 200 moyennes sur
suites de tirages pour
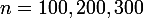
. Voici un exemple de résultats obtenus :
Ce n'est qu'un exemple, et en fait quand on renouvelle l'expérience on constate une assez grande instabilité dans la forme des histogrammes. Il faut aussi se souvenir que les moyennes sont faussées vers le bas par l'écrêtage à 100 000 tirages.
On constate que ça cloche, ou plutôt qu'aucune cloche bien dessinée ne se pointe à l'horizon. Normal, le théorème central limite ne s'applique pas à notre variable aléatoire "temps d'attente du premier retour à l'équilibre" puisque son espérance est infinie.
