Bonjour à tous,
Je suis étudiant en Terminale S et surtout en grand passionné de maths et d'informatique. Je suis en train de créer un puzzle d'algorithmie sur CodinGame mais une clef mathématique me manque pour pouvoir créer une solution optimisée (pas de panique ce n'est pas la partie info qui coince mais la partie mathématique)
Voici donc en quoi consiste le puzzle (Globalement et de manière simplifiée):
On a un score initiale et on doit atteindre un score final, le but est de déterminer le nombre de possibilité d'atteindre le score final à partir du score initial en un nombre de coup définie parla différence score initiale et final.
Je m'explique je suis à 47 je dois attendre 50 donc il y a 3 point de différence ainsi j'aurais 3 tours max pour atteindre ce score ce qui nous donne (Un "/" représente la séparation entre deux tours):
0/0/3
0/3/0
3/0/0
2/1/0
0/2/1
1/0/2
2/0/1
1/2/0
0/1/2
1/1/1
De la même manière si je suis à 46, je veut atteindre 50 (4 points de différence donc 4 tours max pour atteindre le score final)
0/0/0/4
0/0/4/0
0/4/0/0
4/0/0/0
3/1/0/0
. . .
J'apporte une dernière précision à chaque tour on peut marquer au maximum 12 points.
Bref voila donc mon problème, comment à partir de cette différence, je peux arriver à déterminer le nombre de possibilité, car mon problème revient à réfléchir combien de somme égale à la différence peut-on faire.
Je suis parti sur la piste des coefficients binomiaux. Bref dîtes moi tout vos avis m'intéresse !!!
Dénombrement
10 messages
- Page 1 sur 1
Re: Dénombrement
A chaque tour, on peut gagner X points.
Quelles sont les valeurs possibles prises par X ?
je ne comprends pas ce que tu veux dire avec tes colonnes de a/b/c/d/ ou e/f/g/
A voir cette vidéo de Micmaths un peu en rapport avec ton problème :
https://www.youtube.com/watch?v=cGoWEBEEUQw&vl=fr
Quelles sont les valeurs possibles prises par X ?
je ne comprends pas ce que tu veux dire avec tes colonnes de a/b/c/d/ ou e/f/g/
A voir cette vidéo de Micmaths un peu en rapport avec ton problème :
https://www.youtube.com/watch?v=cGoWEBEEUQw&vl=fr
Re: Dénombrement
Merci de ta réponse X peut prendre les valeurs 0,1,2,3,4,5,6,7,8,9,10,11,12
et les colones représentents
Gain premier tour/Gain deuxième tour/Gain troisième tour/. . . /Gain Nième tour
et les colones représentents
Gain premier tour/Gain deuxième tour/Gain troisième tour/. . . /Gain Nième tour
Re: Dénombrement
Salut... on s'est parlé sur Codingames. Je pense avoir la réponse et, ne sachant pas si j'aurai l'occasion de te recroiser sur le site, je t'invite à m'ajouter sur discord : FlyDwen#6275
Re: Dénombrement
@Victorin : chaque colonne est un tour? chaque ligne est un tour? ce n'est pas très clair. Le plus simple serait de représenter l'évolution du score à chaque tour, actualisé.
Remplir un tableau du type :
Numéro de tour : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 ...
Score actuel : x y z t ...................
Remplir un tableau du type :
Numéro de tour : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 ...
Score actuel : x y z t ...................
Re: Dénombrement
Bonjour
Je ne peux pas vraiment y mette sous forme d’un tableau, ce sont juste les différentes possibilités et combinaisons.
Il n’y a aucun lien entre les lignes en revanche oui chaque colonne est un tour
Je ne peux pas vraiment y mette sous forme d’un tableau, ce sont juste les différentes possibilités et combinaisons.
Il n’y a aucun lien entre les lignes en revanche oui chaque colonne est un tour
Re: Dénombrement
Ok, je crois comprendre. Oui il y a une formule, et en plus elle est assez simple.
Si je comprends bien, c'est en fait le problème de combinatoire connu dans la littérature anglo saxonne sous le nom de "Stars and bars".
Tu cherches le nombre de k-uplets de nombres entiers positifs ou nuls de somme fixée N.
On peut montrer que ce nombre vaut exactement N parmi (N+k-1).
A vérifier avec les premières valeurs de k et N.
Attention, tu auras des problèmes d'effets de bord si tu dépasses N = 12 car tu n'autorise pas à gagner plus de 12 points (la formule ne sera donc pas exacte)
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)
ou en français :
http://villemin.gerard.free.fr/Denombre/aaaBalle/Balle01.htm
Si je comprends bien, c'est en fait le problème de combinatoire connu dans la littérature anglo saxonne sous le nom de "Stars and bars".
Tu cherches le nombre de k-uplets de nombres entiers positifs ou nuls de somme fixée N.
On peut montrer que ce nombre vaut exactement N parmi (N+k-1).
A vérifier avec les premières valeurs de k et N.
Attention, tu auras des problèmes d'effets de bord si tu dépasses N = 12 car tu n'autorise pas à gagner plus de 12 points (la formule ne sera donc pas exacte)
https://en.wikipedia.org/wiki/Stars_and_bars_(combinatorics)
ou en français :
http://villemin.gerard.free.fr/Denombre/aaaBalle/Balle01.htm
Modifié en dernier par LB2 le 21 Oct 2019, 22:10, modifié 1 fois.
Re: Dénombrement
Si je comprends bien, ce que tu cherches à calculer est le nombre de façons de ranger  chaussettes indistinguables (les points à gagner) dans
chaussettes indistinguables (les points à gagner) dans  tiroirs (les tours) ?
tiroirs (les tours) ?
Tu représentes par des | les séparations entre tiroirs et pas des x les chaussettes. Par exemple
séparations entre tiroirs et pas des x les chaussettes. Par exemple
xx||x|xxx||x|
représente, avec tes notations
2/0/1/3/0/1/0
Tu es donc ramené à compter le nombres de suites quelconques de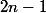 symboles dont
symboles dont  sont des | et
sont des | et  sont des x.
sont des x.
Les coeffcients binomiaux pour compter ça, c'est une bonne idée.
Après, to histoire se complique un peu pour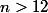 , puisque d'après ce que tu dis on ne peut pas mettre plus de 12 chaussettes dans un même tiroir.
, puisque d'après ce que tu dis on ne peut pas mettre plus de 12 chaussettes dans un même tiroir.
Tu représentes par des | les
xx||x|xxx||x|
représente, avec tes notations
2/0/1/3/0/1/0
Tu es donc ramené à compter le nombres de suites quelconques de
Les coeffcients binomiaux pour compter ça, c'est une bonne idée.
Après, to histoire se complique un peu pour
Re: Dénombrement
Oui c'est un grand classique.
Mot clé : combinaisons avec répétition.
Je vois que tu as eu un petit remord concernant les cas .
. 
Mot clé : combinaisons avec répétition.
Je vois que tu as eu un petit remord concernant les cas
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
