4 doubles d’affilé au monopoly!!!

[fatal_error]

bj,

encore une question que je me pose...

dans l'exemple proposé par gbzm, pour un N donné, et sa somme S obtenue associée: on peut soit augmenter S soit décroitre au lancé N+1.

mais supposons la variante suivante:
qqsoit n, on s'impose une bande centrée en 0 de demi-largeur a...
la somme obtenue S ne doit jamais sortir de cette bande.
quelle est la probabilité d'attendre le lancer k?

edit: comme d'hab je devrais réfléchir avant de poster des questions...( je dois trop suivre le supérieur en ce moment ).

[lyceen95]

@Beagle,
je vois que tu fais des efforts, mais c'est sans espoir, ton ami ne comprend même pas les messages qu'il poste, quand il recopie un bouquin de cours.
Il poste un message qui dit :
Dans une succession de tirages Pile/Face, si on note n=le nombre total de tirages, P=le Nombre de Piles et F=le Nombre de Faces, la probabilité d'avoir P=F est .... et là, on a une formule (exacte, tous les extraits du bouquins sont exacts).

Si on applique la formule du bouquin, pour n relativement grand, disant 1 Milliard, on trouve que la probabilité d'avoir P=F est extrèmement faible, environ 0.01%
Plus loin, le bouquin explique que la valeur la plus probable pour P-F, c'est 0. Tout à fait exact. Intuitif, exact, et démontré. Rien à redire.

Donc ce bouquin dit ; l'événement P=F a une probabilité très faible. Et ton ami transforme ça , en disant ; Puisque l'événement P=F est celui qui a la probabilité la plus élevée, cet événement est quasi certain (la proba de 0.01%, il s'en moque, il ne retient que ce qu'il a envie de retenir...)

Plutôt pisser dans un violon que tenter de raisonner un type aussi buté.

[GaBuZoMeu]

@fatal_error : si tu reformulais clairement ta question, je pourrais essayer d'y répondre. Qui est S, déjà ? C'est P-F que tu appelles S ?

[GaBuZoMeu]

@lyceen95

tous les extraits du bouquins sont exacts

C'est tout de même assez affligeant de voir l'auteur passer par un bricolage ole-ole avec la formule de Stirling pour arriver à la conclusion que est maximum pour si est pair, pour ou si est impair, alors que ça découle immédiatement de .
Sinon, je suis d'accord avec toi pour constater que Dlzlogic se surpasse dans les âneries égrenées dans ce fil.

[fatal_error]

@gbzm,

effectivement, j'ai pas défini S parce que je m'en souciais plus.

on a une marche:
on part de (0,0) dans N^2.
on a les transitions (1,1) et (1,-1)
on veut le nombre de chemins arrivant en (n,i), i allant de -a à a.

les chemins ne doivent jamais atteindre un point (_, a+1) ni (_,-a-1) (idem ils restent dans la bande d'y [-a;a]


sur mes tentatives:
l'approche par matrice me semble velue (les vecteurs propres sont tout plein de chebyshev), donc PDP^-1 pas ouf..
j'ai essayé d'appliquer deux fois le principe de réflexion type:
pour la partie supérieure, je l'applique une fois.
Si je traite le point d'arriver p(n,1)
le chemin passant par (_,a+1) arrivent en a+1 + (a+1-1)
Je fais pareil pour le côté négatif.
Et là où ca colle pas, c'est quand je tente de soustraire les chemins qui ont: d'abord dépassé la borne sup, puis la borne inf et ceux qui ont d'abord dépassé la borne inf puis la borne sup.
pour le premier cas, je dis: en un point (_, a+1) SI je croise aussi la borne inf, alors j'ai parcouru 2*(a+1) vers le bas. Donc si je réfléchis, j'aurais parcouru 3*(a+1) vers le haut. et là, j'applique une deuxième fois le principe de réfléxion pour mon arrivée qui est alors 3*(a+1) + 3*(a+1) - [a+1 + (a+1-1)])
mais je dois avoir une erreur dans le raisonnement... numériquement c'est pas bon.

(je me suis basé sur la démo de ben pour compter les lattice paths superieur/permutation-avec-repetition-t206505.html?hilit=catalan#p1356857)

[GaBuZoMeu]

D'accord, donc ton S était bien le P-F de l'histoire.

Le décompte des chemins de pas qui restent dans la bande se calcule par le principe de symétrie de Désiré André, mais avec tout un tas de miroirs en les . Sauf erreur, on trouve


où
.

(Il est bien entendu que les coefficients binomiaux sont nuls quand ils sortent des clous.

[fatal_error]

hi gbzm,

pour n = 11 et a = 1
les l correspondants sont:

Code: Tout sélectionner

k:0 l:-3
k:1 l:-2
k:2 l:-2
k:3 l:-1
k:4 l:-1
k:5 l:0
k:6 l:0
k:7 l:1
k:8 l:1
k:9 l:2
k:10 l:2
k:11 l:3


pour un k donné, j'ai eu que un seul l donc j'ai juste appliqué:

Code: Tout sélectionner

n = 11
s = 0
for k = 0:n
    low = (2*k-n-2)/4;
    sup = (2*k-n+2)/4;
    while ceil(low) < sup
        l = ceil(low);
        low += 1;
        printf('k:%d l:%d\n', k,l)

        printf('adding %d\n', (-1)^l * nchoosek(n,k))
        s += (-1)^l * nchoosek(n,k);
    end
end
s


Si j'applique la formule j'obtiens ici
2*32 = 64

ce qui semble convenir (on a 32 en (11,1) et le symétrique en (11,-1))

1) En revanche, je comprends pas ce que tu entends par "miroirs". Ni comment tu les construis.
Et Désiré André se fait désirer... je trouve pas non plus de pdf à ce sujet

---------------

2) je détaille mon approche et là où je suis bloqué:

j'ai compté "à la main" les trajets arrivant en (11,-1)
en particulier, les trajets franchissant d'abord la borne sup (up) puis la borne inf (down)
upDown : 54

pour chaque path trouvé à la main, je calcul sont path "symétrique" ex:

Code: Tout sélectionner

   /\       
  /  \     
 /    \     
/......\...
        \   
         \/

                          /<--deuxième sym
                         /
                        / 
                       /   
                      /   
premiere sym  -->/\  /     
                /..\/......


Mais théoriquement j'en compte 55.
En générant tous les paths se terminant en (11,7), je remarque qu'en particulier:

Code: Tout sélectionner

          /
         /
        / 
       /   
      /   
     /     
..../......
\  /       
 \/       



est compté et ne devrait pas, car c'est un trajet downUp et non upDown.

l'approche est donc pas bonne.

Je cherche alors à dénombrer les trajets passant d'abord par up et je bloque

[Ben314]

1) En revanche, je comprends pas ce que tu entends par "miroirs". Ni comment tu les construis.
Et Désiré André se fait désirer... je trouve pas non plus de pdf à ce sujet

Perso., je connais plutôt le bidule sous le terme de "principe de réflexion" plutôt que "principe de symétrie", mais ça change rien au principe (sauf pour chercher sur le net...)
Tu peut trouver le principe en question par exemple là :
http://www.bibmath.net/dico/index.php?a ... rutin.html

[fatal_error]

salut ben,

oui je connais le principe (tu avais déjà donné la démo), mais je vois pas où le(s) appliquer

[Ben314]

J'ai pas du tout cherché à faire des caluls, mais si c'est ça que tu cherche :

on a une marche:
on part de (0,0) dans N^2.
on a les transitions (1,1) et (1,-1)
on veut le nombre de chemins arrivant en (n,i), i allant de -a à a.
les chemins ne doivent jamais atteindre un point (_, a+1) ni (_,-a-1) (idem ils restent dans la bande d'y [-a;a

Alors tu peut procéder comme ça :
1) Tu compte le nombre total de chemin allant de (0,0) à (n,i) avec i dans {-a..a}.
2.1) Tu retranche le nombre de chemin allant de (0,0) à (n,i) avec i dans {-a..a} qui passent au moins une fois par un point (x,a+1) en utilisant le fait qu'il y en a autant que de chemin quelconque allant de (0,0) à (n,i) avec i dans {a+1..3a+1} (principe de réflexion)
2.2) Tu retranche aussi le nombre de chemin allant de (0,0) à (n,i) avec i dans {-a..a} qui passent au moins une fois par un point (x,-a-1) en utilisant le fait qu'il y en a autant que de chemin quelconque allant de (0,0) à (n,i) avec i dans {-a-1..-3a-1} (principe de réflexion)
3) Sauf que, ce faisant, tu as retranché deux fois les chemins qui passent par un (x,a+1) et aussi par un (x',a-1) donc il faut les ré-ajouter et pour se faire considérer deux cas selon qu'on coupe y=a+1 avant ou après y=-a-1.
3.1) Si (x,a+1) est avant (x',a-1) alors tu fait une "double réflexion" : garder intacte la partie du chemin avant le (x,a+1) puis faire une symétrie par rapport à la droite y=a+1 pour la portion comprise entre le (x,a+1) et le (x',a-1) puis faire une double symétrie par rapport à y=-a-1 puis par rapport à y=a+1 pour la fin du chemin (donc une translation de vecteur (0,4a+4). Cette double réflexion te dit qu'il y a autant de chemin qui coupent y=a+1 puis y=a-1 qu'il y a de chemin quelconque allant de (0,0) à (n,i) avec i dans {3a+3..5a+5}
3.2) Idem concernant les chemins tels que (x',-a-1) est avant (x,a+1).
4) Sauf que, ce faisant, tu as retrancha deux fois les chemins qui coupent y=a+1 puis y=-a-1 puis de nouveau y=a+1 (ou le contraire)

etc...

[fatal_error]

yess, j'ai compris l'idée, merci
je vais tenter d'appliquer sur le etc

[GaBuZoMeu]

Je vais raconter ma façon de voir. C'est bien sûr en gros la même chose que ce que raconte Ben, mais avec me semble-t-il quelques petites différences.

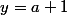
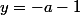
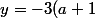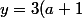Tout d'abord, l'infinité de miroirs : c'est comme dans un ascenseur où il y a des miroirs sur les deux côtés de la cabine. Ici il y a le miroir A à et le miroir B à . Le miroir A se reflète dans B en un miroir A' qui semble à , qui se reflète dans A en A" à etc. De même B se reflète dans A en B' à , qui se reflète en B'' etc.

On compte les chemins qui arrivent en sans toucher les miroirs A et B. Pour cela on compte tous les chemins, et on soustrait ceux qui touchent en premier lieu A et ceux qui touchent en premier lieu B.

Pour compter ceux qui touchent en premier lieu A et arrivent en , on applique le principe de symétrie et on les met en bijection (par symétrie par rapport au miroir A sur toute la partie du chemin suivant le premier contact avec A) avec ceux qui arrivent en (l'image dans le miroir A de ) en touchant en premier lieu A. Puis on compte tous les chemins qui arrivent en et on soustrait ceux qui y arrivent en touchant en premier lieu B.
Pour compter ceux qui touchent en premier lieu B et arrivent en , on les met en bijection (par symétrie par rapport au miroir B sur toute la partie du chemin qui suit le premier contact avec B) avec ceux qui arrivent en en touchant d'abord B. Puis on compte tous les chemins qui arrivent en et on soustrait ceux qui touchent en premier lieu A, etc.
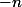
On a ainsi un jeu de ping-pong qui s'arrête quand on dépasse vers le haut ou vers le bas.

On procède de la même façon pour ceux qui touchent en premier lieu B et arrivent en , avec ce ping-pong à nombre fini d'échanges.

On trouve ainsi les alternances de signe qui figurent dans la formule que j'ai donnée plus haut.

J'ajoute une petite image qui explicite les miroirs et les alternances de signe :

[GaBuZoMeu]

Pour fatal_error : un petit code en SageMath qui compte les chemins de longueur n restant dans la bande [-a,a]

Code: Tout sélectionner

def signe(n,a,k) :
    M=(2*k-n+a+1)/(2*(a+1))
    l=floor(M)
    if l==M : return 0
    else : return (-1)^l
   
def chemins(n,a) :
    return add(signe(n,a,k)*binomial(n,k) for k in range(n+1))
   

[GaBuZoMeu]

Une application simple du principe de symétrie de Désiré André.
Au bout de 5000 lancers de pièce (première mi-temps), Pile mène par 2606 contre 2394 pour Face.. Quelle est la probabilité pour qu'au cours des 5000 lancers suivants (deuxième mi-temps) la différence Pile-Face reste toujours supérieure à 100 ?

[GaBuZoMeu]

À propos du P-F qui tend ou pas vers 0 :

Soit la variable aléatoire dont la valeur est la différence entre le nombre de Piles et le nombre de Faces après 1000 lancers de pièces. L'espérance de est 0.
On répète des séries de lancers : on a une suite de variables aléatoires toutes de même loi que , indépendantes.
Alors, presque sûrement, la suite des moyennes converge vers 0 (la probabilité que cette suite converge vers 0 est égale à 1). C'est la loi forte des grands nombres, démontrée par Kolmogorov.

Par contre, ceci ne dit absolument pas que la différence entre le nombre de Piles et le nombre de Faces après N lancers tend vers 0 quand N tend vers l'infini ! Cette assertion est une absurdité complète. Déjà, c'est une suite d'entiers, et une suite d'entiers ne peut tendre vers 0 que si elle est constamment nulle à partir d'un certain rang.

[Sylviel]

Par contre, ceci ne dit absolument pas que la différence entre le nombre de Piles et le nombre de Faces après N lancers tend vers 0 quand N tend vers l'infini ! Cette assertion est une absurdité complète. Déjà, c'est une suite d'entiers, et une suite d'entiers ne peut tendre vers 0 que si elle est constamment nulle à partir d'un certain rang.

Et pour compléter : P-F augmente ou diminue de 1 à chaque tirage. Donc si au rang n elle vaut 0 elle vaudra 1 ou -1 au rang n+1. Elle ne peut donc être constante égale à 0 à partir d'un certain rang

[lyceen95]

Si on est adepte des simulations, on peut aussi en faire :
- On fait 10000 tirages de pile ou face, et on compte P-F
- Et on répète cette expérience 1000 fois.
On trouve donc une série de 1000 nombres (pairs) ... et on constate que ces 1000 nombres ne sont pas tous proches de 0. On obtient une moyenne proche de 0, et un écart-type proche de 100.
Amplitude assez grande quand on s'imagine que cette amplitude doit être de 0.
Bon, peut-être que 10000 tirages, ce n'est pas assez, on va donc faire 40000 tirages (et comme précédemment, répéter cette série de 40000 tirages 1000 fois).
Ca ne s'améliore pas, la moyenne reste proche de 0, mais l'écart-type augmente, alors qu'on aurait voulu qu'il diminue. L'écart-type est mainenant proche de 200.
Tiens , coïncidence ? Dans les 2 expériences, l'écart-type est proche de la racine carrée du nombre de tirages !
Recommençons avec encore plus de tirages, voir si ceci se confirme, ou bien si l'écart-type veut bien diminuer.
90000 tirages dans chaque série, 1000 séries.
Et la tendance se confirme, l'écart-type continue d'augmenter, et il est proche de 300 ... quelle surprise !
Clairement, le nombre P-F ne se rapproche pas de 0 quand on augmente le nombre de tirages, il a plutôt tendance à s'en éloigner.

Mais bien sûr, si on calcule P/F, on se rapproche de 1.
Quand on fait 10000 lancers, on a un rapport P/F qui est proche de 1 ( écart-type = 0.02).
Si on passe à 40000 lancers, l'écart-type est divisé par 2
Si on passe à 90000 lancers, l'écart-type est divisé par 3.

L'écart-type de P/F diminue quand on augmente le nombre de lancers, mais l'écart-type de la différence P-F augmente quand on augmente le nombre de lancers. L'expérience rejoint complètement la théorie.

[fatal_error]

Au bout de 5000 lancers de pièce (première mi-temps), Pile mène par 2606 contre 2394 pour Face.. Quelle est la probabilité pour qu'au cours des 5000 lancers suivants (deuxième mi-temps) la différence Pile-Face reste toujours supérieure à 100 ?

pile a 212 d'avance
rester au dessus de 100 equivaut à pile part de 0 et reste au dessus de -112
au lieu d'avoir une marche de (1; +-2), gardons le classique (1, +-1).
Pile part de (0,0) et reste au dessus de (_, -56)
soient
A nombre de : (1,+1)
B nombre de : (1,-1)
A+B = N
A-B = y
y pair de 0 à N.
la symétrie en y=-k envoie y en -2k-y (donc un offset -2k)

le nombre de chemins où la somme reste positive est donc


C_n^x = 0 pour x > n



en gardant que les cas C_n^x, avec x pair



J'ai pas trouvé comment simplifier...

le nombre de chemins totaux est 2^N
et donc la prob de rester toujours devant pour pile est environ S/2^N = 0.4506315536155099

(j'ai toujours pas fait les miroirs/double sym, pe je regarde cet aprem)

[GaBuZoMeu]

Mouais, un peu faiblichon. C'est ton dernier prix ?
Moi je trouve que la probabilité pour que pile garde toujours plus de 100 points d'avance sur face est de 88,7%.

[fatal_error]

j'ai testé sur des ptits nombres avec monte carlo par ex pour n = 5, et k=-1 (au lieu de -57) je trouve ~0.31 par dénombrement et mc. Je mettrai code à l'appui.

c'est mon ultime bafouille!