Racines doubles d'un polynôme de degré 4

[aviateur]

Bonjour
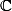
Voici un petit problème apparemment anodin: a et b sont 2 coefficients strictement positifs (a,b>0) et soit P le polynôme défini sur par :



Existe-t-il des valeurs de a et b tel que le polynôme P possède au moins une racine double?

[Arbre]

Bonjour,

Existe-t-il des valeurs de a et b tel que le polynôme P possède au moins une racine double?

Non, car pgcd(P(z),P'(z))=1 (c'est un logiciel qui a fait le calcul pour moi).

[pascal16]

a=0 donne pas mal de solutions

ooups, j'ai oublié le 3

[aviateur]

Bonjour @pascal16. Ici a et b sont strictement positifs.

@arbre tu utilises un logiciel de calcul comme un enfant.
En effet, si je pose la question l'équation ax=1 admet-t-elle toujours une solution, ton logiciel va répondre
oui. En gros c'est ce que tu as fait avec le PGCD de P et P'.

[Arbre]

Puisque messieur râle j'ai utilisé une autre stratégie :

J'ai calculé (avec un pc) : ce qui donne :

{b = 0, a = 1/2*RootOf(-1+3*_Z^2)}, {b = 2*RootOf(_Z^2+2), a = -1/2}, {a = 1/3*RootOf(4*_Z^3+12*_Z^2+9*_Z-1), b = RootOf(_Z^2-1872*RootOf(4*_Z^3+12*_Z^2+9*_Z-1)-1521-612*RootOf(4*_Z^3+12*_Z^2+9*_Z-1)^2)}

RootOf(4*_Z^3+12*_Z^2+9*_Z-1)={0,-3/2}.

Donc si on ne garde que les solutions réels strictements positives, il n'y en a pas.

[Arbre]

en fait une erreur j'ai recalculé : P mod (P' mod (P mod P'))=0

On obtient :

{a = a, b = RootOf(-1+24*a^2-144*a^4+(5+104*a^2+36*a-48*a^3-432*a^4)*_Z^2+(-3888*a^6-7776*a^5-6696*a^4-2784*a^3-659*a^2-114*a-10)*_Z^4+(126*a+1296*a^5+1836*a^3+708*a^2+10+2304*a^4)*_Z^6+(-5-54*a-216*a^4-312*a^3-191*a^2)*_Z^8+(14*a^2+6*a+1+12*a^3)*_Z^10)/a} {b = RootOf(-3+72*a^2-432*a^4+(8+60*a+288*a^2+432*a^3)*_Z^2+(-72*a^2-48*a-7)*_Z^4+(4*a+2)*_Z^6)/a, a = a}

[chan79]

Salut
Juste une conjecture
Pour b égal à 0,5 et pour a environ égal à 3.99383, il y a une solution réelle double égale environ à 0,238
A vérifier (et à démontrer)

[Arbre]

Salut,

@Chan : Ton indication m'a donné du courage, et j'ai tenté avec ma formule et j'ai obtenu :

alors est une racine double

Bonne journée.

[Arbre]

édit : problème sans objet.

[Arbre]

alors est une racine double

@aviateur : et alors je n'ai pas droit au traditionnel : bravo ?

[aviateur]

Bonsoir
A savoir que dans un article, dans un remarque, il avait été conjecturer le contraire.

@Chan tu as raison, j'ai vérifié pour b=1/2 on voit que si a vérifie une certaine équation polynomiale (un peu compliquée ) il y a des racines doubles et la valeur que tu donnes est bien solution approximative de cette équation.
@arbre. Oui c'est bien, il faut le reconnaître. Malheureusement tu mélanges le bien et le moins bien.
Encore ici tu poses une question déjà posée ailleurs et qui n'a aucun lien avec la question ici.

[Arbre]

Bonsoir,

1/Malheureusement tu mélanges le bien et le moins bien.

2/Encore ici tu poses une question déjà posée ailleurs et qui n'a aucun lien avec la question ici.

1/Cela s'appelle apprendre : se tromper, puis tenter de rectifier ses erreurs.

2/C'est ta question qui en est à l'origine.

A savoir que dans un article, dans un remarque, il avait été conjecturer le contraire.

Dans quelle revue ? les réfèrences please.

Au revoir.

[Archytas]

Dans le même genre :

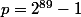
On note avec



Admet-il une racine dans le corps ?

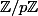
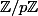
On peut facilement reformuler le problème en disant que ce polynôme a une racine dans si et seulement si il existe 89 entiers consécutifs (modulo p) qui soient tous des carrés.
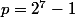
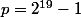
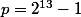
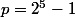
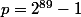
J'ai programmé tout ça, on dirait que ça marche pour et . En revanche ça ne marche pas pour , , . Et le programme est bien trop lourd pour espérer obtenir , je flaire l'utilisation du petit théorème de Fermat derrière tout ça...
Un indice peut-être ?

[Arbre]

Un indice peut-être ?

Le temps a ici sa place.

[chan79]

On peut arriver à des solutions en rajoutant des contraintes.
Avec une racine double réelle égale à b, on a aussi:


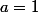
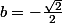
De là à trouver à quelle condition sur le couple de complexes (a,b), l'équation admet au moins une racine complexe double .....

[Arbre]

De là à trouver à quelle condition sur le couple de complexes (a,b), l'équation admet au moins une racine complexe double .....

P mod (P' mod (P mod P'))=0