Limite avec plusieurs variables
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 18:28
par fab_92 » 13 Nov 2006, 18:28
Bonsoir,voila la chose:

avec

>0
En fait, je voudrais surtout savoir la méthode.
Merci d'avance!
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 19:05
par fab_92 » 13 Nov 2006, 19:05
Il y a un problème :look2: ?
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 19:20
par fab_92 » 13 Nov 2006, 19:20
Comment faire pour éviter de tomber sur une forme indéterminée?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 13 Nov 2006, 19:30
par Elsa_toup » 13 Nov 2006, 19:30
Bonsoir,
Je te réponds juste pour que tu ne sentes pas trop seule dans ton malheur : je n'y arrive pas non plus .... :mur:
Mais je cherche.
Tiens bon ! :happy2:
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 19:31
par fab_92 » 13 Nov 2006, 19:31
D'accord. Merci de m'avoir répondu, je me sentais abandonné...
-
Rower
- Membre Relatif
- Messages: 357
- Enregistré le: 09 Nov 2006, 18:09
-
 par Rower » 13 Nov 2006, 19:34
par Rower » 13 Nov 2006, 19:34
Je me penche sur la question (étant débordè jusqu'à présent)
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 13 Nov 2006, 19:38
par nxthunder » 13 Nov 2006, 19:38
Je pense qu'il faut considérer

comme étant une constante, ainsi il te reste plus que la variable x
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 13 Nov 2006, 19:40
par Elsa_toup » 13 Nov 2006, 19:40
Bon je pense qu'on peut déjà transformer ta fraction en:

De là, il ne reste plus qu'à s'occuper de

.
Je pense qu'il faudra arriver à montrer que ça tend vers 0, et le tout tendra alors vers

.
Bon, mais j'y arrive pas encore....

-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 19:42
par fonfon » 13 Nov 2006, 19:42
salut,
on peut essayer de faire:
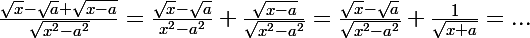
or
}=\frac{(x-a)(\sqrt{x-a})^{-1}}{\sqrt{x+a}(\sqrt{x}+\sqrt{a})}=\frac{\sqrt{x-a}}{(\sqrt{x+a})(\sqrt{x}+\sqrt{a}))
et là plus de forme indeterminée
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 19:48
par fab_92 » 13 Nov 2006, 19:48
D'accord mais j'ai pas suivi la dernière étape...
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 19:58
par fonfon » 13 Nov 2006, 19:58
qu'est ce que tu ne comprends pas?
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 20:06
par fab_92 » 13 Nov 2006, 20:06
Comment tu arrives au dernier résultat?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 20:07
par fonfon » 13 Nov 2006, 20:07
j'ai utilisé l'expression conjuguée
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 20:13
par fab_92 » 13 Nov 2006, 20:13
Désolé, mais peux-tu plus détailler car je suis complètement largué...
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 20:21
par fonfon » 13 Nov 2006, 20:21
Re,
(\sqrt{x}+\sqrt{a})}{\sqrt{x^2-a^2}(\sqrt{x}+\sqrt{a})}=\frac{(\sqrt{x})^2-(\sqrt{a}^2)}{\sqrt{x^2-a^2}(\sqrt{x}+\sqrt{a}))}=\frac{x-a}{\sqrt{x-a}\sqrt{x+a}(\sqrt{x}+\sqrt{a})})
or V(x-a)=(x-a)^(1/2) donc on simplifie avec x-a d'ou le resultat que je t'ai donné
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 13 Nov 2006, 20:23
par fab_92 » 13 Nov 2006, 20:23
Ok pour l'expression conjuguée mais pourquoi x²-

² devient

?
Ok, je l'ai. Merci.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Nov 2006, 20:43
par fonfon » 13 Nov 2006, 20:43
ça y est tu as compris?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 177 invités