Potentiel vecteur et champ scalaire
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
Maxx1805
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Aoû 2018, 20:54
-
 par Maxx1805 » 28 Aoû 2018, 16:45
par Maxx1805 » 28 Aoû 2018, 16:45
Bonjour, voilà, j'ai deux potentiel vecteur tel que
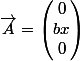
et

reliés par la relation
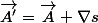
et je dois trouvez le champ scalaire

dont le gradient quand il est ajouté à
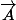
donne
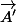
.
Mes résultats sont
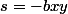
Est-ce juste et pourrais-je avoir une méthode s'il vous plaît.
J'ai oublié de dire que ces deux potentiel vecteur engendre le même champ magnétique (
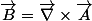
)
-
aviateur
 par aviateur » 28 Aoû 2018, 18:04
par aviateur » 28 Aoû 2018, 18:04
C'est clair que s répond à la question. Une méthode? c'est de l'intégration toute simple
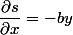
d'où
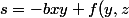= -b xy +g(y))
(car
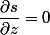)
puis tu exploites la deuxième ligne...
i.e
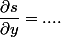
-
Maxx1805
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Aoû 2018, 20:54
-
 par Maxx1805 » 28 Aoû 2018, 18:55
par Maxx1805 » 28 Aoû 2018, 18:55
Excuse moi, mais que signifie
)
, est-ce une constante? Si je suis ce raisonnement
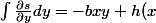)
-
aviateur
 par aviateur » 28 Aoû 2018, 19:58
par aviateur » 28 Aoû 2018, 19:58
Non tu intègres par rapport à x donc ça fait -bxy + "expression qui ne dépend pas de x mais dépend de y,z "
notée f(y,z). Mais d'après la troisième ligne ça ne dépend pas de z donc f(y,z) cela ne dépend que de y seulement et je note cette fonction de y g(y)
-
Maxx1805
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Aoû 2018, 20:54
-
 par Maxx1805 » 28 Aoû 2018, 20:05
par Maxx1805 » 28 Aoû 2018, 20:05
Alors question qui peut sembler bête mais peut on inscrire un champ scalaire a l'aide de ses composantes en x,y,z.
Sinon je ne comprends pas la suite des calculs à faire pour arriver s=...
-
aviateur
 par aviateur » 28 Aoû 2018, 20:21
par aviateur » 28 Aoû 2018, 20:21
inscrire ? je en comprends pas.
Tu as s=-bxy+g(y)
d'après la deuxième ligne
\partial s/\partial y=-bx =-bx+g'(y)
Donc g'(y)=0 , i.e g(y)=cste
Finalement s=-bxy +cste.
-
Maxx1805
- Membre Naturel
- Messages: 25
- Enregistré le: 21 Aoû 2018, 20:54
-
 par Maxx1805 » 28 Aoû 2018, 21:11
par Maxx1805 » 28 Aoû 2018, 21:11
Ok merci pour ton aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités