Champ potentiel (distribution linéique )
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
khadi8
- Membre Relatif
- Messages: 102
- Enregistré le: 20 Aoû 2009, 12:33
-
 par khadi8 » 07 Mai 2010, 17:32
par khadi8 » 07 Mai 2010, 17:32
salut j'ai une question sur la solution de la 1ere question de mon exercice le voici
une tige isolante de longueur L porte une charge Q uniformément répartie en longueur (densité charge linéique )
01/ déterminer le champ électrique produit par cette tige au point P , d'abscisse X

ma question est la suivante
quand on fait la projection sur (xx') on obtient
dEp=2dEx i ou bien
dEp=dEx i
la quelle des deux est juste ??et pourquoi ??le reste je sais faire
mercii
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Mai 2010, 17:39
par Arnaud-29-31 » 07 Mai 2010, 17:39
Bonjour,
C'est quoi ton i ?

est le champ élémentaire créé par le morceau de tige centré en M et de longueur dy, qu'on pourra ensuite intégrer entre -L/2 et L/2 pour avoir
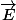
En revanche sur ton schéma, ce qui est noté

vaut

avec

le champ élémentaire créé par le morceau de tige centré sur le symétrique de M par rapport à O. Et donc

vaut

... Ce

est donc à intégrer entre 0 et L/2 puisque quand M décrit [0,L/2], M' décrit [-L/2,0]
-
khadi8
- Membre Relatif
- Messages: 102
- Enregistré le: 20 Aoû 2009, 12:33
-
 par khadi8 » 07 Mai 2010, 18:27
par khadi8 » 07 Mai 2010, 18:27
le i c le vecteur unitaire
voici ma solution complète a vous de corrigé
dEM=2k&dl/r² cos(Q)
l=x tgQ et cosQ=x/r
dl=x*1/cosQ dQ
donc
dEM= 2k&/x integrale entre (L/2 et -L/2) cos Q dQ
= 2k&/x [sinQ]
= 2k&/x (L/2/(L/2)²+x²)
=2k&/x (L/2/(L/2)²+x²)^1/2
Q veut dire téta
& veut dire lambda
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Mai 2010, 18:56
par Arnaud-29-31 » 07 Mai 2010, 18:56
C'est trèès dur a déchiffrer ...
Je suppose que

S'il y a le facteur 2, cela veux dire que l'on considère que

est la résultant de deux champs élémentaires créés par deux morceaux de tiges symétriques par rapport à O.
Il faut donc comme je l'ai dis dans mon précédent post intégrer entre 0 et L/2.
On arrive donc bien à
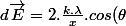.d\theta)
à intégrer entre 0 et
)
On fera disparaître le

pour faire apparaître Q.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
