La différence entre un Corps et un Anneau

[grantstewart]

Bonjour à tous...

Je sais que Corps et Anneaux correspondent à la construction de systèmes munis d'opérations et de lois, faisant intervenir des ensembles. Mais pouvez-vous préciser la différence entre les deux ?

[pascal16]

dans les deux (K,+) est un groupe
dans un corps : pour la loi * chaque élément, sauf 0, admet un inverse
dans un anneau, ce n'est pas vrai (cf les matrices ou un Z/nZ avec n non premier)

[grantstewart]

Pouvez-vous préciser, expliquer ???

[pascal16]

tu sais multiplier deux matrices ?

une matrice avec un déterminant nulle n'est pas inversible.
c'est à dire M existe, mais pas 1/M.

[grantstewart]

NON, JE NE SAIS PAS MULTIPLIER 2 MATRICES...

[mathelot]

bonsoir,
voir le lien: https://fr.wikipedia.org/wiki/Produit_matriciel

[grantstewart]

x

[danyL]

dans les deux (K,+) est un groupe
dans un corps : pour la loi * chaque élément, sauf 0, admet un inverse
dans un anneau, ce n'est pas vrai (cf les matrices ou un Z/nZ avec n non premier)

pascal16,
Tes explications sont vagues, non-pertinentes et sans intérêt.
Si hdci pouvait intervenir, ce serait bien.
Je veux une réponse claire à ma question ci-dessous.

Je sais que Corps et Anneaux correspondent à la construction de systèmes munis d'opérations et de lois, faisant intervenir des ensembles. Mais pouvez-vous préciser la différence entre Corps et Anneaux ?

quand tu auras compris, tu auras le droit de t'excuser platement

[hdci]

Comme l'a dit Pascal16 : la principale différence entre un anneau et un corps, c'est que la loi qu'on appelle "multiplicative" (en référence aux ensembles de nombres) possède un inverse pour tout élément non nul.

Autrement dit : si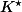 représente l'ensemble K privé de l'élément neutre de l'addition (donc de 0), alors

• est un anneau si est un groupe abélien (commutatif), et si la loi multiplicative est associative, distributive sur l'addition (c-à-d : et
• "Dans le temps", cela suffisait et on parlait d'anneau unitaire lorsque la loi multiplicative avait un élément neutre, mais je crois que de nos jours on oblige l'anneau à avoir un élément neutre multiplicatif.
• est un corps si c'est un anneau et si de plus est un groupe abélien

Exemples :

• est un anneau (dit "commutatif" car la multiplication est commutative), mais ce n'est pas un corps car par exemple 2 n'a pas d'inverse dans
• est un corps car est un groupe abélien, la multiplication es distributive sur l'addition et est un groupe abélien
• De même pour et

Il y a bien d'autres anneaux et corps, mais les exemples précédents sont les exemples fondamentaux (qui ont sûrement servi de base à ces définitions de structures d'ensemble)

[Elias]

Salut,

Je me place dans le cas des anneaux commutatifs pour ne pas compliquer les choses.

Un anneau (commutatif unitaire) est un ensemble A muni de deux lois notées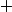 et vérifiant un certain nombre de propriétés que je ne vais pas énumérer ici (que l'on trouve facilement sur le net).
L'anneau est alors noté parfois

En particulier, il y a deux éléments qui sont à part :
- un premier élément noté aussi appelé "l'élément neutre pour la loi "
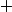C'est un élément qui est tel que pour tout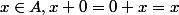
- un deuxième élément noté aussi appelé "l'élément neutre pour la loi ". C'est un élément qui est tel que pour tout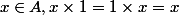


Maintenant, posons nous la question suivante: si je prends un élément quelconque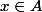 , est-il possible de trouver un autre élément 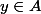tel que ??
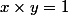Si jamais c'est possible, on dira alors que est inversible (ou que possède un inverse).

Exemple: dans l'anneau , l'élément 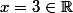est inversible. En effet, il est possible de trouver 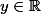tel que 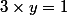. Il suffit de prendre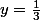

En revanche, l'élément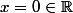 n'est pas inversible. On aura beau chercher des heures et des heures, on ne trouvera aucun 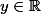tel que 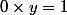puisque 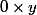fait toujours

Si on réfléchit bien, dans ce cas particulier de l'anneau , pour n'importe quel nombre 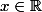sauf 0,il sera possible de trouver un inverse de


Autre exemple: dans l'anneau , l'élément 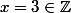n'est pas inversible.
En effet, on peut chercher là aussi des heures, impossible de trouver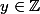 tel que 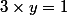(le seul y qui convient n'est pas un nombre dans 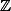puisqu'il n'est pas entier).

En revanche, l'élément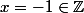 est inversible puisque 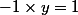avec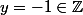



Revenons au cas général :
si je prends un anneau et que je prends au pif un élément 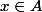, alors j'ai deux possibilités :
- soit possède un inverse ;
- soit n'en possède pas.
Nous sommes également sûr d'un truc (qui peut se démontrer en utilisant la distributivité): c'est que n'a jamais d'inverse dans n'importe quel anneau (sauf l'anneau nul éventuellement mais on s'en fout)

Attention, on arrive à la conclusion du post :
Il existe des anneaux pour lesquels TOUS LES ÉLÉMENTS (SAUF 0) sont inversibles. C'est typiquement le cas de l'anneau comme évoqué plus haut. Ces anneaux vérifiant cette propriété sont appelés des corps .


Ainsi est un corps tandis que n'en est pas un.


Dernière remarque: dans tout le post, je parle d'UN inverse mais on peut démontrer que si un élément admet UN inverse, alors il en admet QU'UN seul et donc il y a unicité de l'inverse.

[hdci]

Elias et moi nous sommes croisés...

J'ajoute un dernier point que j'ai passé sous silence dans ma définition : un corps possède au moins deux éléments (ceci dit cela "tombe sous le sens" puisque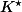 n'est pas vide : l'ensemble vide n'est pas un groupe).

alors que l'anneau nul est bel et bien un anneau, même si ici tous les éléments sont inversibles puisque l'élément neutre additif est également l'élément neutre multiplicatif !

[grantstewart]

Merci beaucoup Elias & hdci !
Voici de belles et claires explications...

[Yezu]

Bonjour,

1/ Tu pollues le feed des topics avec de gros trolls pseudo physique
2/ La recherche personnelle t'aurais donné une réponse en moins de 15 secondes avec n'importe quel moteur de recherche (il y a même déjà eu ce topic sur maths-forum ..)
3/ Pascal prend son temps pour te donner une réponse valide
4/ Tu réfutes sa réponse en la considérant comme bancale.
5/ Tu insistes sur sa réponse """bancale""" avec tes remerciements pour Elias et hdci.

Quel est l'intérêt de venir sur un forum, troller, poser des questions auxquelles on trouve réponse sur internet en 15 s, réclamer formellement des réponses de la part d'une unique personne et tacler les autres intervenants ?

Je ne suis pas de la modération, ni de l'administration, mais comme danyL, j'espère que tu prendras conscience qu'envisager des excuses pour le très aimable Pascal serait la moindre des choses.

[grantstewart]

x

[pascal16]

excuses acceptées

j'avais utilisé les matrices car elle sont vues au lycée, alors que les autre notions sont vues en post bac.

[grantstewart]

x

[grantstewart]

x

[Yezu]

Mouais je vois pas en quoi tu fais avancer quoique ce soit en maths sans la moindre tentative de recherche personnelle (qui répond à toutes les questions que tu te poses).

Pour ta pseudo physique, je préfère ne même pas en parler.

[grantstewart]

x

[Yezu]

Évidemment.