Equivalent d une suite

[houssamhoussni]

salut,
comment calculer l'equivalent de la suite definie par:
uo=a dans R
u(n+1)=u(n)+exp(-u(n))
merci!

[Ben314]

Salut,

(1) est croissante et, si elle tendait vers 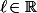on aurait 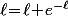ce qui est absurde.
Donc elle tend vers l'infini, mais très lentement vu que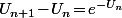 tend vers 0.

(2) Il est naturel de poser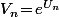 un peu du fait que ça apparaît déjà dans la formule de départ, mais surtout du fait que, si avec f "assez régulière" alors, vu la croissance de plus en plus lente de vers +oo, on a qui doit être très proche de donc l'équation de départ est plus ou moins qui est une équation différentielle facile à résoudre avec comme solution .
(Si j’écris tout ce blabla. c'est qu'il s'applique dans pas mal de cas et qu'il donne trés souvent une bonne idée d'un équivalent de la suite de départ)

(3) On pose donc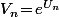 (qui est >0 et tend vers +oo vu que tend vers +oo) et on a .
Il suffit alors d'utiliser des encadrement de pour voisin de 0 (et >0) pour déduire à peu prés tout ce qu'on veut...

P.S. On peut savoir quel mouche te pique pour que tu mette un tel problème dans la section "Physique" ?