Bonjour à tous,
Question facile j'imagine, dans beaucoup d' exercices on fait le changement de variable en polaire, dans la correction il y a toujours marqué, par exemple: on remarque que: x^2+y^2 < 1 ssi 0<r<1 et 0<theta<2pi
( les "<" sont des "inférieur ou égal", je n'ai pas voulu trop alourdir une assertion aussi simple )
Pour moi ce n est pas évident du tout, comment ré-exprime t'on le domaine d'intégration quand on fait un changement de variable de ce genre? De quoi peut-t'on partir?
De prime abord je ne vois pas ce qui me permettrait d'écrire x^2 + y^2 <1 , donc on a 0<x<1 et 0<y<1 soit
[0,1]X[0,1]...
Et même en faisant cela je ne vois pas comment en déduire dans quelle intervalle se trouve theta puisque avec le chgt de variable en polaire j ai x = rcos(theta) ; y = rsin(theta).
Merci d'avance.
Intégrales multiples
8 messages
- Page 1 sur 1
Re: Intégrales multiples
Bonjour !
"toujours marqué" et "par exemple" ce n'est pas très cohérent !
Si que vaut
que vaut 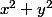 ?
?
Pour les limites de il faut regarder un dessin de l'ensemble où tu dois faire l'intégration...
il faut regarder un dessin de l'ensemble où tu dois faire l'intégration...
Faire un dessin, c'est d'ailleurs la première idée qui devrait s'imposer...
"toujours marqué" et "par exemple" ce n'est pas très cohérent !
Si
Pour les limites de
Faire un dessin, c'est d'ailleurs la première idée qui devrait s'imposer...
Re: Intégrales multiples
Kolis a écrit:Bonjour !
"toujours marqué" et "par exemple" ce n'est pas très cohérent !
Sique vaut
?
Pour les limites deil faut regarder un dessin de l'ensemble où tu dois faire l'intégration...
Faire un dessin, c'est d'ailleurs la première idée qui devrait s'imposer...
Bonjour Kolis, merci pour ta réponse,
ok j'éviterai de mélanger "toujours marqué" et "par exemple" ^^
oui
Je commençais à me dire que sur un dessin c est évident, r est entre 0 et 1,
Et lorsqu'on aura à faire à un intervalle trop compliqué pour faire un dessin, quelle sera la solution?
Modifié en dernier par yoshi13 le 09 Avr 2017, 15:05, modifié 1 fois.
Re: Intégrales multiples
Salut,
Quand on manipule un truc, il faut toujours en avoir la définition en tête (ça me semble être le mini du mini).
Et la définition des coordonnées polaires "de base" (*), ça consiste à voir que la fonction\mapsto(r\cos\theta,r\sin\theta)) est un C^1 difféomorphisme de l'ouvert
est un C^1 difféomorphisme de l'ouvert  sur l'ouvert
sur l'ouvert  où
où  est la demi droite (fermée)
est la demi droite (fermée)  .
.
Bref, par définition même de ce que sont "les coordonnées polaires", on a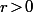 .
.
(*) Modulo des "variantes" par exemple en prenant comme intervalle pour un autre intervalle de largeur
un autre intervalle de largeur  ce qui conduit à enlever une autre demi-droite que
ce qui conduit à enlever une autre demi-droite que  à l'arrivé.
à l'arrivé.
Ensuite, il n'y a( heureusement) pas qu'un dessin à faire pour justifier les intervalles où doivent être situés et
et  (le dessin peut aider, mais n'est souvent pas considéré comme une preuve).
(le dessin peut aider, mais n'est souvent pas considéré comme une preuve).
Ici, via la bijection citée çi dessus, équivaut à
équivaut à  donc à
donc à  vu que le domaine de définition de la bijection en question, c'est
vu que le domaine de définition de la bijection en question, c'est  .
.
Ensuite, concernant , il n'y a aucune contrainte vu que l'inéquation
, il n'y a aucune contrainte vu que l'inéquation  ne contient pas de
ne contient pas de  donc on prend tout le domaine de définition de la fameuse bijection, à savoir
donc on prend tout le domaine de définition de la fameuse bijection, à savoir 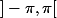 (ou
(ou 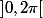 si c'est ça qu'on à choisi comme domaine de définition de la bijection en question)
si c'est ça qu'on à choisi comme domaine de définition de la bijection en question)
Non, surement pas.yoshi13 a écrit:mais alors r est entre -1 et 1, pas 0 et 1.
Quand on manipule un truc, il faut toujours en avoir la définition en tête (ça me semble être le mini du mini).
Et la définition des coordonnées polaires "de base" (*), ça consiste à voir que la fonction
Bref, par définition même de ce que sont "les coordonnées polaires", on a
(*) Modulo des "variantes" par exemple en prenant comme intervalle pour
Ensuite, il n'y a( heureusement) pas qu'un dessin à faire pour justifier les intervalles où doivent être situés
Ici, via la bijection citée çi dessus,
Ensuite, concernant
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intégrales multiples
Ben314 a écrit:Salut,Non, surement pas.yoshi13 a écrit:mais alors r est entre -1 et 1, pas 0 et 1.
Quand on manipule un truc, il faut toujours en avoir la définition en tête (ça me semble être le mini du mini).
Et la définition des coordonnées polaires "de base" (*), ça consiste à voir que la fonctionest un C^1 difféomorphisme de l'ouvert
sur l'ouvert
où
est la demi droite (fermée)
.
Bref, par définition même de ce que sont "les coordonnées polaires", on a.
(*) Modulo des "variantes" par exemple en prenant comme intervalle pourun autre intervalle de largeur
ce qui conduit à enlever une autre demi-droite que
à l'arrivé.
Ensuite, il n'y a( heureusement) pas qu'un dessin à faire pour justifier les intervalles où doivent être situéset
(le dessin peut aider, mais n'est souvent pas considéré comme une preuve).
Ici, via la bijection citée çi dessus,équivaut à
donc à
vu que le domaine de définition de la bijection en question, c'est
.
Ensuite, concernant, il n'y a aucune contrainte vu que l'inéquation
ne contient pas de
donc on prend tout le domaine de définition de la fameuse bijection, à savoir
(ou
si c'est ça qu'on à choisi comme domaine de définition de la bijection en question)
Excellent! Merci Ben pour ton explication.
Effectivement tu as raison c'est indispensable d'avoir la définition, j'avais l esprit si embrouillé que je n'en ai même pas tenu compte

Je reviendrai probablement sur ce topic pour d'autres domaines d'intégration car j'ai encore quelques soucis pour les intégrales entre deux courbes, j'ai du mal a définir sur quel ensemble intégrer, savoir comment encadrer y par rapport a x et vice versa.
Encore merci
Re: Intégrales multiples
On pourrait prendre  dans ce cas on aurait
dans ce cas on aurait  pour ne pas couvrir 2 fois le disque.
pour ne pas couvrir 2 fois le disque.
Re: Intégrales multiples
@pascal16
Pour faire un changement de variables il faut une fonction dont le jacobien ne s'annule pas !
Si r a le droit de changer de signe cette condition ne sera pas satisfaite.
Pour faire un changement de variables il faut une fonction dont le jacobien ne s'annule pas !
Si r a le droit de changer de signe cette condition ne sera pas satisfaite.
Re: Intégrales multiples
oui... et non...Kolis a écrit:@pascal16
Pour faire un changement de variables il faut une fonction dont le jacobien ne s'annule pas !
Si r a le droit de changer de signe cette condition ne sera pas satisfaite.
Pourvu que ta fonction soit effectivement bijective, si le jacobien s'annule sur des ensembles de mesure nulle (au départ et à l'arrivé), ça ne va pas poser de problème pour faire un changement de variable dans une intégrale.
De façon purement formelle, il te suffit d'enlever les points où il s'annule du domaine de définition de ta bijection et tu va pouvoir appliquer le théorème : dans ta paramétrisation, il te manquera juste des "morceaux", mais comme ces "morceaux manquant" comptent pour du beurre dans l'intégrale, ça ne changera rien.
Et cette histoire de ne pas tenir compte des "morceaux qui comptent pour du beurre", ben faut déjà l'utiliser pour justifier que les coordonnées polaires "usuelles" (c.f. post çi dessus) marchent pour n'importe quelle intégrale alors que la paramétrisation "évite" toute une demi droite de R^2 (on pourrait éventuellement songer à prendre un intervalle du style [0,2.pi[ fermé en 0 pour théta de façon à "mieux couvrir" R^2, mais il manque toujours (0,0) et en plus dans ce cas, la bijection réciproque n'est même pas continue donc ce n'est surement pas un C^1 difféo.)
Bref, accepter r négatif (mais pas r=0) et restreindre theta à un intervalle (ouvert) J de largeur pi, ça change rien concernant le principe : dans ce cas, on a un C^1 difféo de R*x J sur R^2 privé d'une droite.
Pour moi, le seul problème, c'est au niveau du vocabulaire, c'est à dire de savoir si on continue à appeler ça "un changement de variable polaire" ou si on va plutôt dire que c'est du "pseudo-polaire"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
