DÉNOMBREMENT ET COMBINAISONS ( tour de Hanoï)

[peed]

Bonjour,
J’ai de mal à répondre aux questions suivantes

Sachant qu'on part d'une tour de Hanoï. 3 tours et n disques
Soit Sn la suite de coups permettant de déplacer les n disques d'une tour vers une autre. On note cn le nombre de coups de Sn

Question 1 Combien de bits sont nécessaires et suffisants pour coder un coup possible (en supposant qu'il y ait un disque dans chaque tour et que l'on puisse jouer de n'importe quelle tour vers n'importe quelle autre tour en empilant un disque sur un disque pas nécessairement plus grand) ?

Question 2 en utilisant le codage de la question précédente, avec combien de bits peut-on coder la suite Sn des coups permettant de déplacer n disques ?

Question 3 Combien existe-t-il de façons de placer les 5 disques répartis sur les trois tours. On ne considérera que les placements corrects, c'est-à-dire que sur chaque tour les disques sont empilés par taille décroissante de bas en haut. Deux placements sont différents si on peut trouver un disque qui n'est pas dans la même tour dans les deux placements.

Question 4 Combien existe-t-il de façons de placer les 9 disques de sorte à ce qu'il y ait 3 disques sur chaque tour. On ne considérera que les placements corrects.

Question 5 Combien existe-t-il de façons de placer sur les trois tours :
— n disques de manière correcte ?
— n disques, éventuellement de manière incorrecte ?

Question 6 On souhaite maintenant coder un placement correct de n disques sur les trois tours. Peut-on coder ce placement avec 2n bits ? Justifiez votre réponse.

Question 7 Combien existe-t-il de façons de placer les 6 disques de sorte à ce qu'il y ait 2 disques sur chaque tour. On considérera cette fois-ci tous les placements possibles même ceux qui ne sont pas corrects. Cela signifie que les disques ne sont pas forcément empilés par taille décroissante de bas en haut. Deux placements sont différents si on peut trouver un disque qui n'est pas à la même position (en partant du haut) dans une tour dans les deux placements ou si on peut trouver un disque qui n'est pas sur la même tour dans les deux placements.

Question 8 On souhaite maintenant coder un placement (pas nécessairement correct) de n disques sur les trois tours. Peut-on coder ce placement avec 2n[log(n)] bits ? En cas de réponse positive donner le codage et en cas de réponse négative donner un argument prouvant l'impossibilité d'un tel codage.

[pascal16]

j'y connais rien, je déteste les tours de Hanoï, mais je me lance
Q1:
liste des déplacements possibles
1->2, 1->3,2->1, 2->3, 3->1,3->2
3 bits (= 8 cas) semblent donc être un minimum

Q2 : à un décalage d'indice près : 3n

[Ben314]

Salut,
Perso, ça m'aurait aussi intéressé de savoir... ce que tu avais fait et dans quelle voie tu était allé...
Sinon, a mon avis,
- Pour le 1), la réponse attendue est effectivement "3 bits".
- Par contre, pour le 2), j'aurais répondu sans hésiter : 3 bits par coups et coups pour décrire .

Et les question 3) et 4) sont clairement là pour te faire tâtonner en faisant des dessins ou tout autre truc facile à faire dans le cas où il n'y a que 5 (ou 9) disques de façon à introduire la question 5.
Donc c'est on ne peut plus con qu'on te donne les réponses.

[peed]

pour la Q1 j'ai trouver la formule qui permet de calculer le nombre de bits
Les déplacement possible sont : 3!=6 on trouve ainsi 3 bits

[Dasson2]

Bonjour,
Peut aider ?
http://rdassonval.free.fr/flash/hanoibi.swf
https://www.youtube.com/watch?v=xN3DNAc_88A

[peed]

pour la Q 3 j'ai trouvé :

pour la Q 4 j'ai trouvé :

[Ben314]

Oui, c'est bien ça : Si on ne cherche que les placements "corrects" alors il suffit de savoir sur quelle tour sont placés les différents disque vu que sur une tour donnée il n'y aura pas le choix concernant l'ordre dans lequel les disques sont placés.

Ensuite, la première question de Q5, c'est assez évident maintenant que tu as fait Q3.
Pour la deuxième question, une façon de procéder, c'est de commencer par regarder combien il y a de façon de placer tout les disques sur la première tour (facile) puis de regarder le nombre de façon qu'il y a de scinder la première pile en 3 sous piles qu'on va mettre sur les 3 tours (là, c'est moins évident si on a jamais vu "l'astuce" pour dénombrer ce genre de truc).

P.S. Au vu du résultat de la deuxième question, il y a une autre façon de procéder plus simple : regarder le nombre de façon de placer le 1er disque, puis le deuxième, puis le troisième, etc...

[peed]

bonjour
tu veux dire que la réponse de la premier question de Q5 vaut : ?

[Ben314]

bonjour
tu veux dire que la réponse de la premier question de Q5 vaut : ?

Oui.
C'est la deuxième question qui est plus compliquée, mais en considérant qu'on place les disques les uns après les autres, ça se fait.

[peed]

Bonjour

pour la question 7 : c'est bon ?

[Ben314]

Pour la 5)b) j'aurais répondu (n+2)!/2

Pour la 6) j'aurais répondu OUI car 3^n <= 2^(2n)

pour la question 7 : c'est bon ?

Par contre, pour la 7), j'aurais répondu : choix des 2 disques parmi les 6 sur la première tour puis des 2 disque parmi les 4 restant pour la deuxième tour puis pas le choix ()pour la 3em tour et enfin choix sur chaque tour de l'ordre dans lesquels on place les deux disques (2! possibilités pour chacune des 3 tours).
Si tu as vu les arrangements, ça correspond bien sûr à .
Et au final, ça vaut en fait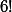 ce qui est logique vu que pour entièrement décrire la situation, il suffit dire qui est le disque du haut de la première pile, puis qui est le disque du bas de la première pile, puis qui est le disque du haut de la deuxième pile, etc...

[peed]

moi je pense que :
nombre de bits
dans notre cas : le nombre de bits
nombre de bits