Probabilités conditionnelles - Niveau TS

[Alx59]

Bonjour les matheux !

Je me suis arraché le peu de cheveux qu'il me restait sur la dernière question 4) de cet exo de proba (confère fichiers en PJ, que je vous ai entièrement retapés sous Word pour être plus lisible ).

Ca me semble être du niveau Terminale S. Je ne vois pas du tout par où commencer la dernière question :

- ce sont des probas conditionnelles
- il y a 2 conditions, l'une est dans le passé (mes parents ont le gêne r tous les 2) et l'autre dans le futur (mon fils a également le gêne r). Et la question est au "présent" : quelle proba que moi aussi j'ai le gêne r sachant ces 2 conditions ?

J'ai essayé avec un arbre, par le calcul, etc. mais rien n'y fait, je suis bloqué.

Pourriez-vous me dépanner svp ? Je suis très curieux de voir comment faire

Merci,
Amicalement,
Alex

[Sulaheia]

Hello,

Tu peux mettre tes réponses aux premières questions stp ?
Normalement, ça va donner des pistes pour la suite.

[Alx59]

Hello Sulaheia,

Oui, je te donne ce que j'ai trouvé avec le raisonnement qui va avec (après, à voir si c'est correct) :

1) Comme on nous dit hypothèse C les couples se forment au hasard, les événements sont indépendants et on peut multiplier les probas entre elles :

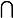
p(A1) = p(RRp RRm) = p(RRp) x p(RRm) = (1-)²
p(A2) = x (1-)
p(A3) = p(A2)
p(A4) = ²

2) Pour la première génération parvenue à l'âge adulte, on recherche donc p(Rr). Il faut voir la proba que les adultes aient formé certains types de couples (cf. question 1) associée aux probas données dans l'hypothèse A :

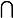
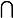
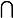
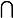
p(Rr) = p(A1 Rr) + p(A2 Rr) + p(A3 Rr) + p(A4 Rr)
p(Rr) = p(A1) x pA1(Rr) + p(A2) x pA2(Rr) + p(A3) x pA3(Rr) + p(A4) x pA4(Rr)
p(Rr) = (1-)² x 0 + x (1-) x x 2 + ² x

Soit, après avoir simplifié :
p(Rr) = x (1-)

3)
a/ Si mon frère est mort portant rr, j'en déduis que mes parents sont A4. On cherche donc la proba p(Rr) sachant A4, que je note pA4(Rr) :

pA4(Rr) = qu'on tire directement de l'hypothèse A.

b/ On nous parle de premier-né qui meurt car rr. J'ai donc fait un arbre :
- le premier niveau c'est moi, avec 2 branches, 1 où je suis Rr, l'autre où je ne le suis pas.
- le second niveau c'est la femme que j'ai rencontré, une où elle est Rr, l'autre où elle ne l'est pas.
- le troisième et dernier niveau, c'est mon enfant, avec une branche où il est rr et meurt, et l'autre branche tous les autres cas.

Il n'y a qu'un seul chemin de l'arbre qui mène à un décès de mon premier enfant : je suis Rr, ma femme est Rr, et mon gosse rr.

Donc, si je me considère moi et ma femme comme faisant partie des adultes, j'ai :
p(rr) = =

Si je considère que je suis parmi la 1ère génération parvenue à l'âge adulte, alors p(Rr) vaut le résultat de la question 2) et j'ai :
p(rr) =
p(rr) =

Je ne sais pas quel résultat est le bon pour cette question.

4) Nous y voilà enfin, là je n'ai aucune idée de comment modéliser ça correctement... Toute aide ou piste est la bienvenue

Merci d'avance, en espérant que je n'ai pas pris la peine de taper tout ça pour rien, si vous avez des idées !

[Ben314]

Salut,
Je ne suis d'accord ni avec ton 2), ni avec ton 3) :

Pour le 2), si tu fait exactement le même type de calcul pour p(RR) (à la génération 2), tu va trouver que p(rR)+p(RR) n'est pas égal à 1 et ceci pour la bonne et simple raison que le même calcul donnerais un p(rr) non nul alors que, vu la question posée "fréquence des porteurs de gènes parvenus à l'age adulte", tu devrais indubitablement trouver que p(rr)=0 vu qu'il n'y a pas d'adultes rr.

Même erreur pour le 3) où le calcul que tu fait correspond en fait à la question "quelle est la proba que l'éventuel prochain gosse de mes parents soit Rr" et ce n'est pas la même chose que la question "quelle est la proba que je soit Rr" vu que le prochain gosse de tes parents, il pourrait être rr (donc mort né) alors que toi, ben tu sait que tu n'est pas mort né...
Par exemple, en supposant qu'absolument tout les porteurs du gène r (donc les Rr et les rr) donnent des morts-né à ta génération (et pas à la précédente où tes parents sont nés) alors, rien que de savoir que tu est vivant te donnerais une proba de 1 d'être RR alors que toi, avec ton calcul, tu ne trouverais qu'une proba de 1/4.

[Alx59]

Salut Ben,

Merci pour ta réponse.

2) en effet, j'arrive à la somme des probas égale à 1 - lambda² /4
Je pense que p(rr) vaut lambda² / 4 justement. Mais comme on s'intéresse aux personnes vivantes en effet, comment intégrer ça dans le calcul ?

J'ai comme intuition de reprendre mes probas trouvées et pour transformer ça en fréquence, de faire :
fréquence ( Rr ) = p(Rr) / ( p(Rr) + p(RR) )
fréquence ( rr ) = 0
fréquence ( RR ) = 1 - fréquence ( Rr)

3) puis-je faire pareil ici ?
le fait de savoir que mon frère soit mort né me donne comme indication que mes parents sont A4.
+ la déduction que moi, je suis vivant, ça réduit à 2 options : B1 et B2

donc p(Rr) = p(B2) / ( p(B1) + p(B2) ) = 0.5 / 0.75

Pour le b/, qu'en penses-tu ?

Encore merci pour tes remarques, je pensais pourtant avoir bon aux premières questions. Il me faut encore un peu plus de recul sur ces probas

[Ben314]

Concernant le 2) et le 3), c'est effectivement, c'est comme ça que je ferais, ce qui correspond en fait à faire des proba. conditionnelles.
Dans les deux cas on conditionne par du "sachant que ce n'est pas du rr" vu qu'on parle d'adultes et que cela élimine les morts-nés c'est à dire les rr du calcul.

Pour le b), la proba demandée, c'est effectivement :
proba(je suis rR, mon conjoint aussi et mon gosse est rr)
Comme les eux premiers trucs sont supposés être indépendant, ça donne :
proba(je suis rR) x proba(mon conjoint est rR) x proba(mon enfant est rr sachant que moi et mon conjoint sont rR)
- La première proba, on vient de la calculer.
- La troisième proba, on te dit que c'est 1/4 (arbre donné)
- Par contre, il y a ambiguïté concernant la deuxième proba vu que ça dépend de la génération à laquelle appartient ton conjoint : s'il est de "génération initiale", la proba qu'il soit rR est lambda (hypothèse B), mais, s'il est (comme toi), de la "première génération", alors la proba qu'il soit rR est celle trouvée à la question 2).
Perso, j'aurais sans doute tendance à considérer que mon conjoint est de la même génération que moi, mais c'est pas complètement clair...

[Alx59]

Coucou,

Merci pour ta confirmation !
Oui, le b) est sujet à interprétation, mais la logique des choses veut qu'il y ait des couples "sains" avec environ le même âge donc même génération et on reprend la fréquence / proba trouvée à la question 2).

Et donc, on en arrive à la question 4), as-tu une idée de comment modéliser ça sous forme de proba ?

J'ai noté sur mon brouillon proba( je suis Rr SACHANT QUE [mon fils est Rr ET mon frère rr]), mais je n'ai de mémoire jamais eu affaire à des proba conditionnelles avec 2 conditions.

Peut-on dire que c'est = p(mon fils Rr ET mon frère rr ET je suis Rr) / p(mon fils Rr ET mon frère rr) ?
Comment poursuivre ensuite ?

[Ben314]

- Mon Frère est mort rr => mes parents sont tout les deux Rr.
- Mon petit fils est mort rr => mon fils/ma fille est forcément Rr (et son conjoint aussi) => de moi et de mon conjoint, un (au moins) des deux est Rr.
Donc j'aurais tendance à penser que ce qu'il faut calculer, c'est la proba conditionnelle :
proba(je suis Rr sachant qu'avec mon conjoint, au moins un des deux est Rr)
Et il suffit plus ou moins d'écrire que p(A sachant B)=p(A et B)/p(B) pour déterminer cette proba.

[Alx59]

Je ne suis pas d'accord avec ton calcul, car si l'énoncé était simplement "mon petit fils est mort rr" tu arriverais au même calcul.

Or, il est bien précisé en plus que mon frère est mort rr. Donc il faut en plus intégrer l'hypothèse des parents qui sont tous les 2 Rr. Et on en arrive à une sorte de double condition.

J'ai l'intime conviction qu'il faut se servir des résultats des questions précédentes, mais j'vois pas comment...

Avec un arbre, les branches sont simples, on distingue bien les différents cas. Mais comment traduire ça dans un calcul ? Je t'ai représenté mon arbre en PJ.

[Ben314]

Je ne suis pas d'accord avec ton calcul, car si l'énoncé était simplement "mon petit fils est mort rr" tu arriverais au même calcul.

Non, je n'arriverais pas à la même chose vu que le calcul de la proba que je sois Rr ne donne pas la même chose selon qu'on sait ou pas que mes parents sont Rr tout les deux :
La proba que je soit Rr (sachant que j'ai eu un frère rr) est
La proba que mon conjoint soit Rr (sachant qu'il est le la 2em génération) est
Donc, vu l'indépendance supposée,
1) La proba qu'on soit Rr tout les deux est .
2) La proba que je sois Rr et pas lui est .
2) La proba qu'il soit Rr et pas moi est .
Donc la proba que je soit Rr sachant qu'un (au moins) des deux l'est est

[Alx59]

Salut Ben,

J'ai refait l'exo avec un pote, et je viens de le refaire tout seul, avec mes connaissances et tes remarques.

Déjà, bonne nouvelle, j'ai tout compris, merci

Pour être serein, il me reste 2 3 petits détails :
- la question 3) a/, comment peut-on noter la proba conditionnelle "proba que je sois Rr sachant que mes parents sont A4 ET que je ne suis pas rr) ?

Est-ce que c'est correct de mettre ça : P(Rr) ?
J'ai l'impression que non, car si on fait un arbre, ça n'a pas de sens.

- la question 4), j'arrive au même résultat que toi avec l'arbre suivant :

Maths exo 5.png (12.09 Kio) Vu 542 fois

J'ai calculé : P(je suis Rr sachant que mon fils est Rr) = somme des probas des chemins avec moi Rr et mon fils Rr / somme des probas des chemins avec mon fils Rr

Ce qui revient à faire ton calcul, mais uniquement si on prend une proba de 1/2 que mon fils soit Rr sachant que ses parents sont tous les deux Rr (1/2 en rouge dans le graphique). Or, ne devrait-on pas prendre 2/3 au lieu de 1/2 car on sait que notre fils est vivant ?

**EDIT : après réflexion, ton calcul de P(je sois Rr sachant qu'au moins un des 2 l'est) me semble inexact. Il ne tient pas compte du fait que ton fils est forcément vivant, car tu as un petit-fils. Ton calcul correspondrait plutôt à la condition "mon fils est Rr ou rr", je me trompe ? C'est pour ça que je prendrais plutôt 2/3 dans mon arbre au lieu de 1/2 pour le premier cas (moi Rr et ma femme Rr). **

En dehors de ça, tout le reste me paraît clair !

[Ben314]

- la question 3) a/, comment peut-on noter la proba conditionnelle "proba que je sois Rr sachant que mes parents sont A4 ET que je ne suis pas rr) ?
Est-ce que c'est correct de mettre ça : P(Rr) ?
J'ai l'impression que non, car si on fait un arbre, ça n'a pas de sens.

Pour moi, si tu veut calculer
p=probaje suis Rr sachant que (mes parents sont A4 et je ne suis pas rr)
la seule autre "façon de l'écrire" qui me semble éventuellement utile, c'est

qui est plus ou moins la définition de la notion de proba conditionnelle.
Et dans un exo pareil, j'aurais tendance à éviter comme la peste tout les raccourcis d'écriture comme d'écrire "RR" à la place de "je suis RR" vu les risques d'erreurs que ça peut provoquer (comment tu va écrire ensuite "mon conjoint est RR" ou "mon fils est RR" ?) et donc évidement dans ce cas, il faut écrire es ET et des OU et pas des et des pour que ce soit cohérent avec la formulation.

EDIT : après réflexion, ton calcul de P(je sois Rr sachant qu'au moins un des 2 l'est) me semble inexact. Il ne tient pas compte du fait que ton fils est forcément vivant, car tu as un petit-fils. Ton calcul correspondrait plutôt à la condition "mon fils est Rr ou rr", je me trompe ? C'est pour ça que je prendrais plutôt 2/3 dans mon arbre au lieu de 1/2 pour le premier cas (moi Rr et ma femme Rr).

Perso, l'info "mon petit fils est mort rr", je l'ai traduite comme disant uniquement"je sais que mon fils est Rr" puis comme "je sais que moi ou mon conjoint est Rr" c'est à dire comme intervenant en temps que "proba conditionnelle".
Mais je me demande effectivement si l'info "j'ai un fils Rr" et l'info "moi ou mon conjoint est rR" sont équivalentes en terme de proba, donc je me demande si ce n'est pas toi avec ton 2/3 qui a raison, c'est à dire que l'info "j'ai un fils Rr VIVANT" n'a pas tendance à augmenter la proba de "je suis Rr et mon conjoint aussi" par rapport à l'info "moi ou mon conjoint est Rr". Sauf que j'en mettrais pas ma main à couper non plus.
Bref, désolé, mais je sais pas trop...

[Alx59]

Coucou Ben, merci pour ta réponse.

Pour le premier point, ça ne me paraît pas très intuitif d'écrire ça comme ça. J'ai du mal à comprendre la logique derrière cette "division" de probas. Pourtant, si je fais le calcul en utilisant les formules des probas conditionnelles, j'arrive en effet plus ou moins à la proba qui est demandée.

Ce que j'aurai eu tendance à noter de base :

P( Rr moi / (parents A4 ET rr barre moi) ) =

Avec ta notation, ça me donne :

p =

p =

p =

Donc on arrive quasi à la même chose.
Je partage ton avis, ce genre de notation est à bannir pour ce genre d'exo. Pour ne pas me gourer, j'utilise les indices "p", "m", "f"... suivant de qui ou quelle génération on parle.

Le second point, pour info, effectivement, ça semble augmenter la proba de considérer 2/3. Pour chaque question, je me suis amusé à tracer le résultat obtenu des P(...) en fonction de lambda variant entre 0 et 1.

Déjà, bonne nouvelle, quel que soit lambda entre 0 et 1, nos probas sont aussi comprises dans cet intervalle. Et pour la 4), si on considère 1/2 ou 2/3, on obtient 2 courbes quasi identiques, avec celle du 2/3 légèrement au-dessus de celle de 1/2. Ca maximise donc la proba d'être Rr si on considère que notre fils est vivant et qu'on prend 2/3 sur l'arbre.

Voilà, je pense qu'on a fait le tour du sujet. (sauf si un jour on s'amuse à généraliser tout ça pour les arrières arrières arrières.... petits fils ^^).