Exercices niveau 2nd
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par mathsforever » 10 Sep 2016, 22:02
par mathsforever » 10 Sep 2016, 22:02
bonjour tout le monde ! j'ai besoin de votre aide pour un exercice d'algèbre :
Soit x un réel, on pose a =

.
Prouver que a, b,

sont pour tout x compris dans l'intervalle [-1;1]
Merci de votre soutient

.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 22:23
par Razes » 10 Sep 2016, 22:23
Ils ont le même dénominateur. calcule

 par mathsforever » 10 Sep 2016, 22:31
par mathsforever » 10 Sep 2016, 22:31
oui mais avant de régler le problème de

, j'aimerai bien régler celui de a et b avant.

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 22:39
par Razes » 10 Sep 2016, 22:39
Que peux tu dire de:
^2)
 par mathsforever » 10 Sep 2016, 23:00
par mathsforever » 10 Sep 2016, 23:00
^2)
? c'est une identité remarquable. J'ai même essayer de factoriser
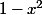
ce qui me donne : (1-x)(1+x) mais je suis face à un mur

-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 11 Sep 2016, 00:29
par Razes » 11 Sep 2016, 00:29
^2\geqslant 0\\ et\\(x+1)^2\geqslant 0\end{matrix}\right. \Rightarrow \left\{\begin{matrix}x^2+1\geqslant 2x\\ et\\ x^2+1\geqslant -2x\end{matrix}\right.\Rightarrow \left\{\begin{matrix}x^2+1\geqslant 2x\\ et\\ 2x\geqslant -\left (x^2+1 \right )\end{matrix}\right.\Rightarrow \dfrac{\left |2x \right |}{x^2+1}\leqslant 1)
CQFD
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 11 Sep 2016, 12:01
par Pseuda » 11 Sep 2016, 12:01
Bonjour,
Tu peux commencer par montrer que

et

sont tous deux

1 (si tu veux d'abord traiter a et b).
La suite sera facile.
 par mathsforever » 11 Sep 2016, 18:07
par mathsforever » 11 Sep 2016, 18:07

Très bonne idée, un nombre dont le carré est inférieur à 1 est compris dans l'intervalle -1 ;1

merci !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
 Très bonne idée, un nombre dont le carré est inférieur à 1 est compris dans l'intervalle -1 ;1
Très bonne idée, un nombre dont le carré est inférieur à 1 est compris dans l'intervalle -1 ;1