0,9999... = 1

[Mohwali Awamar]

C'est tout le problème.Tendre vers zéro ne signifie pas l'egalité avec zéro .L'égàlité est avec epsilon zéro. 2epsilon zéro =]+0,-0[
Mohwali Awamar

[Romy]

D'aucuns, pourtant enseignants aux lycées, confondent encore la notion d'états dynamiques avec les résultats.
Revoir la lim : Xn->L dans R ssi : quelque soit epsilon >0, il existe n0 tel que : |xn-L| < epsilon, pour tout n >= n0.
Romy

[Pseuda]

D'aucuns, pourtant enseignants aux lycées, confondent encore la notion d'états dynamiques avec les résultats.
Revoir la lim : Xn->L dans R ssi : quelque soit epsilon >0, il existe n0 tel que : |xn-L| < epsilon, pour tout n >= n0.
Romy

Quelle est pour toi la différence entre "notion d'états dynamiques" et "résultats" ? Quelles sont leurs définitions mathématiques ?

Je suppose que tu veux parler de la limite. Pour moi, une limite finie ce n'est, ni plus ni moins, qu'un nombre, dont se rapprochent les valeurs prises par une fonction ou une suite.

L'écriture 0,9999.... (avec des petits points qui signifient que le 9 part à l'infini) signifie très exactement (ou, si tu préfères, est une manière plus rapide d'écrire) : . Et cette limite est égale à 1.

Tout est dit dans cette discussion : cafe-mathematique/incoherence-t132322.html (voir notamment ce que dit Sylviel).

[Romy]

Tendre vers zéro ne signifie pas l'égalité avec zéro .L'égalité est avec epsilon zéro. 2epsilon zéro =]+0,-0[

L'approximation que donne la calculatrice ne vaut pas la limite: 0,00.....1= 10^(-n) où : n := {nombre de 0 lus+1}.
Ainsi: 10^{-1000000000} n'égale pas 0. Or, on aura : lim{n->00}(Xn)=1 dans R ssi : quel que soit epsilon >0 (ex: epsilon=10^{-59876321}), il existe n0 (ex: n0=10^1000000000) tel que : |xn-1| < epsilon et pour tout n >= n0.
Romy

[Pseuda]

Tendre vers zéro ne signifie pas l'égalité avec zéro .L'égalité est avec epsilon zéro. 2epsilon zéro =]+0,-0[

L'approximation que donne la calculatrice ne vaut pas la limite: 0,00.....1= 10^(-n) où : n := {nombre de 0 lus+1}.
Ainsi: 10^{-1000000000} n'égale pas 0. Or, on aura : lim{n->00}(Xn)=1 dans R ssi : quel que soit epsilon >0 (ex: epsilon=10^{-59876321}), il existe n0 (ex: n0=10^1000000000) tel que : |xn-1| < epsilon et pour tout n >= n0.
Romy

Bonjour,

Ce n'est pas cela. 0,00......1 écrit comme cela, est la limite de 10^(-n) quand n-> oo, donc c'est égal à 0. Revois ton cours sur les développements décimaux illimités.

[Romy]

L'approximation que donne la calculatrice ne vaut pas la limite: 0,00.....1= 10^(-n) où : n := {nombre de 0 lus+1}.

Cf. un cours de 6ème de collège sur la division : "La division décimale permet, à partir d’un dividende et d’un diviseur, d’obtenir soit un quotient décimal exact (nombre de chiffres après la virgule défini), soit une valeur approchée du quotient (nombre de chiffres après la virgule infini)." Or, 1/3 est dans Q qui inclut D qui inclut N.
Romy

[beagle]

bah entre 0,9999... et 1 il n' y a rien
et c'est bien parce qu'il n'y rien = pas de place entre les deux, géométriquement c'est plus facile,
que les deux points sont confondus sur une ligne numérique .

[Pseuda]

L'approximation que donne la calculatrice ne vaut pas la limite: 0,00.....1= 10^(-n) où : n := {nombre de 0 lus+1}.

Cf. un cours de 6ème de collège sur la division : "La division décimale permet, à partir d’un dividende et d’un diviseur, d’obtenir soit un quotient décimal exact (nombre de chiffres après la virgule défini), soit une valeur approchée du quotient (nombre de chiffres après la virgule infini)." Or, 1/3 est dans Q qui inclut D qui inclut N.
Romy

Bonjour,

J'ai l'impression que tu ne connais pas les développements décimaux illimités (série qui converge vers un réel, défini à partir de ses décimales). Cela n'a rien à voir avec la division euclidienne (avec quotient et reste), et c'est différent de la division décimale (développement décimal limité, qui donne une valeur exacte ou approchée du quotient, et qui s'arrête).

Tandis que le développement décimal illimité, comme son nom l'indique ne s'arrête pas. Pour plus de précisons :

https://www-fourier.ujf-grenoble.fr/~ro ... eChap4.pdf

Ce n'est pas une notion abordée au collège....

Voir dans le document l'exemple de la définition 4.2 qui affirme que : 1 = 0,9999..... (avec une suite de 9 qui part à l'infini), et que ce développement est un développement impropre de 1, tandis que 1,0000.... (avec une suite de 0 qui part à l'infini) est un développement propre de 1. Un réel ne peut admettre qu'un et un seul développement propre.

De manière générale (et de mémoire), on introduit les réels, soit à partir des rationnels (réel = classe d'équivalence de suites convergentes de rationnels), soit à partir des développements décimaux illimités.

As-tu compris cette fois ?

[Eliza]

Ô coucou !

C'est plus pédagogique de dire que : "Lorsque les nombres sont des entiers naturels, le développement décimal correspond à leur écriture en base 10. Lorsqu'ils sont décimaux, le développement décimal est limité. Lorsqu'ils sont rationnels, un développement décimal illimité périodique s'obtient. Lorsque les nombres sont irrationnels, le développement décimal est illimité et non périodique". Voilà à quoi rimera la leçon du cours extraite du Wiki !

Bon vent...

[nodgim]

Contrairement à Beagle, je ne vois rien à redire à l'égalité 1/3 = 0,333....
Sinon, il y aurait beaucoup de choses à remettre en cause...

[Pseuda]

Petite remarque par rapport à une question que je me suis posée : le nombre 0,00...001 (= 1 - 0,9999... ) n'est pas l'écriture d'un développement décimal illimité, car dans ce développement, la décimale 1 est remplacée par 0 au fur et à mesure. C'est juste la limite de 10^(-n) avec n qui tend vers l'infini, donc c'est 0.

[beagle]

Contrairement à Beagle, je ne vois rien à redire à l'égalité 1/3 = 0,333....
Sinon, il y aurait beaucoup de choses à remettre en cause...

Je ne vois rien à redire non plus ...

[beagle]

Contrairement à Beagle, je ne vois rien à redire à l'égalité 1/3 = 0,333....
Sinon, il y aurait beaucoup de choses à remettre en cause...

Je ne vois rien à redire non plus ...

Tu veux dire que t'es d'accord avec beagle?

[beagle]

perso ce qui me gène est plutôt ceci=
le nombre 0,00...001 (= 1 - 0,9999... )
pas assez de connaissance mais je trouve cela bizarre,
je préfère imaginer que ce 1 final n'existe pas dans le 0,9999... qui est le 1 entier.
mais bon je ne sais pas faire la soustraction infinie donc ce que j'en dis ...

[Pseuda]

perso ce qui me gène est plutôt ceci=
le nombre 0,00...001 (= 1 - 0,9999... )
pas assez de connaissance mais je trouve cela bizarre,
je préfère imaginer que ce 1 final n'existe pas dans le 0,9999... qui est le 1 entier.
mais bon je ne sais pas faire la soustraction infinie donc ce que j'en dis ...

Bonjour,

Cela vient de ce que le terme de la série est : , c'est-à-dire :
1 - 0,9 = 0,1 ; 1 - 0,99 = 0,01 ; 1 - 0,999 = 0,001 ; etc...

Mais cette série n'est pas un d.d.i. quand n tend +oo, car les décimales ne sont pas "acquises". Dans le cas contraire, ce serait inquiétant car un réel aurait un nombre infini de d.d.i. de ce genre (en contradiction avec la théorie).

EDIT : perso, ce serait plutôt de dire "il n'y a rien entre 0,9999.... et 1" qui me gênerait ; si, il y a 0,000...1, avec le 1 qui part à l'infini. Mais bon, finalement, tout cela n'est qu'un jeu d'écriture.

[beagle]

Bonjour Pseuda,
mon approche est à prendre avec des pincettes puisque mon niveau est celui de fin de collège.
Donc intuitivement je ferais une différence entre tendre vers l'infini et ètre l'infini.
Dans le 0,999... les 9 sont infinis, il n' ya pas à tendre vers.
De sorte que plutôt que de voir un espace qui se réduit (je suis plus a l'aise avec une dimension), cela tend vers du plus petit (l'écart entre du 1 et des 0,99 où on allonge les 9),
je préfère d'emblée y voir un :il n'existe pas n tel que 10^-n est l'écart avec 1.
Il n' y a pas d'écart à 1 versus l'écart à 1 se réduit ...
Mais bon, si avec les outils maths c'est idem ou plus rigoureux, je m'incline bien volontiers.

[beagle]

"perso, ce serait plutôt de dire "il n'y a rien entre 0,9999.... et 1" qui me gênerait ; si, il y a 0,000...1, avec le 1 qui part à l'infini. Mais bon, finalement, tout cela n'est qu'un jeu d'écriture."

peut-être que l'on se rapproche des discussions sur la valeur des démonstrations par l'absurde.
Beaucoup de matheux de grande qualité du site n'aiment pas trop cela.
Il me semble ètre souvent plus à l'aise avec ce raisonnement.
Il me semble souvent plus facile de comprendre que les choses ne peuvent pas ètre telles que ... plutôt que de comprendre d'emblée pourquoi alors elles sont ceci cela.

Et ici 0,999... ne peut pas ètre autre chose que 1 car il n'existe pas ce fameux 0,000001 ou autre plus loin, plus loin,... ben il n' y en a pas.C'est parce que pas que l'égalité.
C'est plus facile pour moi que de comprendre dans l'autre sens...

Mais bon là je suis peut-être plus tordu que la moyenne dans ma façon de raisonner...
Je sais pas, et en plus je fais ce que je peux!

[samoufar]

Bonjour,

Juste deux petites choses :

1- Même en suivant cette logique, je ne vois pas pourquoi (l'écriture équivaut à ). Déjà que , alors avec un "nombre" plus petit (je pense que tu parlais plutôt de );

2- Le "nombre" n'a pas de sens mathématique ou de sens logique. En effet, si tu dis qu'il y a un après les , c'est que tu connais la position de ce , donc que l'infini est quantifiable donc fini (sinon, où est-ce que vient ce ? Autant, pour , on comprend plus ou moins logiquement l'infinité de , mais là un après une infinité de ...), mais le "nombre" ne l'est pas.

D'ailleurs pour revenir sur les commentaires précédents, le nombre est bien défini comme somme d'une série (la série des 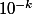à un facteur près).

Mais bon, pour bien comprendre ça, il faut d'abord savoir ce que signifient les notions de limite et de série

[Pseuda]

Bonjour,

Juste deux petites choses :

1- Même en suivant cette logique, je ne vois pas pourquoi (l'écriture équivaut à ). Déjà que , alors avec un "nombre" plus petit (je pense que tu parlais plutôt de );

Hum c'est l'ambiguïté de la phrase : "il y a c entre a et b", qui te fait écrire cela. Cette phrase peut se comprendre par "il existe un nombre c compris entre a et b", ou bien on peut vouloir parler de la différence c=a-b. C'est évidemment dans ce 2ème sens que j'entends "entre 1 et 0,999....., il y a 0,00.....1"

2- Le "nombre" n'a pas de sens mathématique ou de sens logique. En effet, si tu dis qu'il y a un après les , c'est que tu connais la position de ce , donc que l'infini est quantifiable donc fini (sinon, où est-ce que vient ce ? Autant, pour , on comprend plus ou moins logiquement l'infinité de , mais là un après une infinité de ...), mais le "nombre" ne l'est pas.

D'ailleurs pour revenir sur les commentaires précédents, le nombre est bien défini comme somme d'une série (la série des à un facteur près).

Mais bon, pour bien comprendre ça, il faut d'abord savoir ce que signifient les notions de limite et de série

Ce 0,000...1 est une écriture (pas forcément académique, je l'avoue, et qui n'est pas un d.d.i.) de : limite 10^(-n) quand n tend vers +oo (par analogique avec 0,999... qui est l'écriture de la limite de la série). Tout cela, je le répète, n'est qu'une écriture, rien de plus.

[beagle]

bon faut bien que je rabaisse un peu le débat.
Il ya un soucis d'espace temps avec ce truc de 0,000...1 qui manque toujours:
il manquerait toujours si toujours qui est une notion temporelle.
Or la définition (j'imagine, j'y connais couic, mais pourquoi pas) de la somme infinie des 9,
n'est pas une somme temporelle:
on ne fait pas 0
puis 0+0,9
puis 0,9+0,09
puis0,99 +0,009
puis
puis puis c'est temporel.

or dans somme des trucs 9 de 1 à l'infini, la somme est déjà faite merci, la définition est instantanée, t=0 j'ai tous les 9 de placés
donc on ne va pas chercher à repousser où on pourrait mettre le 0,000...1
tous les 9 sont instantanément là, ya pas de place pour du 1 et puis c'est marre.
bref la somme de la série est une réunion ensembliste de tous les 9, c'est pas une opération faite par un supercalculateur une addition après l'autre...
C'est l'observation de la somme qui amène cette temporalité qui ne devrait pas exister...
Bon c'est modeste comme contribution, mais le il y a toujours un écart petit peti de plus en plus petit,
non pas de plus en plus, instantanément il n'y a pas d'écart.