Bonjour à tous.
Dans le cadre du cours du mathématiques, nous faisons des études de fonctions. La première étape consiste donc à définir le domaine de f. Cependant, pour un exercice, j'ai un souci et je ne sais comment m'y prendre. Voici l'énoncé :
f(x) = (2x+1) / 4x²
Selon moi, la condition d'existence serait : 4x² ≠ 0.
Ensuite, je ne sais pas du tout comment m'y prendre pour arriver à une valeur chiffrée...
Ça donnerait :
4x² ≠ 0
x² ≠ 0 / 4
x ≠ Racine de 0 / 4
x ≠ 0
Je serait vraiment très étonné si vous me répondiez que je procède de la bonne façon... Je sens que mon raisonnement n'est pas le bon donc je fais appel à vous.
Je vous remercie d'avance pour vos réponses.
Mathématiques - Domaine d'une fonction.
10 messages
- Page 1 sur 1
Re: Mathématiques - Domaine d'une fonction.
salut
la condition d'existence est effectivement
mais on ne résout pas ce genre de "non égalité" mais l'équation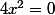
et depuis le collège je sais que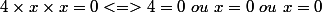
...
la condition d'existence est effectivement
mais on ne résout pas ce genre de "non égalité" mais l'équation
et depuis le collège je sais que
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Mathématiques - Domaine d'une fonction.
Je vous remercie zygomatique.
Cela voudrait dire que le domaine de f serait :
Dom f : R \ {0}
Serait-ce correct ?
Cela voudrait dire que le domaine de f serait :
Dom f : R \ {0}
Serait-ce correct ?
Re: Mathématiques - Domaine d'une fonction.
oui ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Mathématiques - Domaine d'une fonction.
Je ne voudrais pas abuser de votre gentillesse mais j'aurais encore des questions pour la suite de l'étude de cette fonction... Au niveau de l'asymptote verticale, je trouve une asymptote verticale ayant comme équation : x = 0 (logique).
Par contre, je bloque dans la recherche d'asymptotes horizontales... Pourriez-vous m'aiguiller s'il vous plait ?
D'avance merci !
Par contre, je bloque dans la recherche d'asymptotes horizontales... Pourriez-vous m'aiguiller s'il vous plait ?
D'avance merci !
Re: Mathématiques - Domaine d'une fonction.
Bonsoir,
Quelle est la limite de f en l'infini? (+ infini et -infini)?
Que penser de la droite y=0
Quelle est la limite de f en l'infini? (+ infini et -infini)?
Que penser de la droite y=0
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Mathématiques - Domaine d'une fonction.
Bonsoir Lostounet et merci de votre réaction à mon post.
1/ Limite de f en + l'infini = + l'infini / + l'infini.
Limite de f en - l'inifini = - l'infini / - l'infini = l'infini / l'infini.
J'ai donc les mêmes limites pour + et - l'infini.
Mais pas de valeur numérique... Il y a-t-il donc une asymptote horizontale en + l'infini ?
2/ Je ne sais pas par où commencer pour répondre à cette question
1/ Limite de f en + l'infini = + l'infini / + l'infini.
Limite de f en - l'inifini = - l'infini / - l'infini = l'infini / l'infini.
J'ai donc les mêmes limites pour + et - l'infini.
Mais pas de valeur numérique... Il y a-t-il donc une asymptote horizontale en + l'infini ?
2/ Je ne sais pas par où commencer pour répondre à cette question

Re: Mathématiques - Domaine d'une fonction.
Attention, bien que ton calcul soit a priori cohérent, la limite de la forme infini/infini est une forme indéterminée.
(la deuxième ce serait -infini/+infini à cause du x carré)
Cela signifie que, diviser un truc infiniment grand par un truc infiniment grand donne...rien! On ne peut pas savoir.
10000/10000000000 est proche de 0 alors que le numérateur est "grand" et le dénominateur aussi.
10000000000/10000 est très grand alors que le num et le dénominateur sont "grands". La notion de "grand" est donc relative.
Tout dépend de l'ordre de grandeur des quantités divisées.
Exemple: quelle est la limite de (x^2/(x+1)) en l'infini?
Il est vrai que c'est de la forme infini/infini mais le x^2 croit beaucoup plus vite que x. Cela signifie qu'à terme, c'est le numérateur qui va l'emporter.
Plus mathématiquement, on parle de "lever l'indétermination" en rendant compte de ce phénomène. On peut penser à prendre x en facteur et simplifier, par exemple:
(x^2/(x+1) = x*x/(x(1+1/x)) = x/(1+1/x)
En l'infini 1/x tend vers 0, donc le quotient se comporte comme x/1: tend vers +infini.
Il se trouve que dans ton exo, c'est l'inverse qui se produit.
F(x) = (2x+1) / 4x²
Prenons x en facteur:
F(x)=x(2+1/x)/x*x = (2+1/x)/x
1/x tend vers 0 donc le quotient se comporte comme 2/x en l'infini et donc tend vers....
Moralité: la réponse infini/infini n'est pas satisfaisante. Il faut regarder qui croit plus rapidement, numérateur ou dénominateur?
(la deuxième ce serait -infini/+infini à cause du x carré)
Cela signifie que, diviser un truc infiniment grand par un truc infiniment grand donne...rien! On ne peut pas savoir.
10000/10000000000 est proche de 0 alors que le numérateur est "grand" et le dénominateur aussi.
10000000000/10000 est très grand alors que le num et le dénominateur sont "grands". La notion de "grand" est donc relative.
Tout dépend de l'ordre de grandeur des quantités divisées.
Exemple: quelle est la limite de (x^2/(x+1)) en l'infini?
Il est vrai que c'est de la forme infini/infini mais le x^2 croit beaucoup plus vite que x. Cela signifie qu'à terme, c'est le numérateur qui va l'emporter.
Plus mathématiquement, on parle de "lever l'indétermination" en rendant compte de ce phénomène. On peut penser à prendre x en facteur et simplifier, par exemple:
(x^2/(x+1) = x*x/(x(1+1/x)) = x/(1+1/x)
En l'infini 1/x tend vers 0, donc le quotient se comporte comme x/1: tend vers +infini.
Il se trouve que dans ton exo, c'est l'inverse qui se produit.
F(x) = (2x+1) / 4x²
Prenons x en facteur:
F(x)=x(2+1/x)/x*x = (2+1/x)/x
1/x tend vers 0 donc le quotient se comporte comme 2/x en l'infini et donc tend vers....
Moralité: la réponse infini/infini n'est pas satisfaisante. Il faut regarder qui croit plus rapidement, numérateur ou dénominateur?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Mathématiques - Domaine d'une fonction.
Autre exemple illustratif.
Vers quoi tend f(x)=(x^2+1)/(2x^2+1)?
Prenons x^2 en facteur:
F(x)=(x^2(1+1/x^2))/(x^2(2+1/x^2))
= (1+1/x^2)/(2+1/x^2)
À l'infini, 1/x^2 tend vers 0. Donc f va tendre vers... 1/2!
Alors qu'a priori on avait du infini/infini. En effet on constate après coup que le numérateur et le dénominateur ont la même "force" (alors qu'avant il y avait une puissance écrasant l'autre).
Lever l'indétermination pour des fractions rationnelles est souvent simple: c'est toujours la même astuce, on met en facteur la plus grande puissance possible et on observe. Mais ce n'est pas toujours très simple de lever une indéterimination par exemple pour des fractions irrationelles:
superieur/factorisation-racine-carree-pour-exo-sur-les-limites-t173449.html
Vers quoi tend f(x)=(x^2+1)/(2x^2+1)?
Prenons x^2 en facteur:
F(x)=(x^2(1+1/x^2))/(x^2(2+1/x^2))
= (1+1/x^2)/(2+1/x^2)
À l'infini, 1/x^2 tend vers 0. Donc f va tendre vers... 1/2!
Alors qu'a priori on avait du infini/infini. En effet on constate après coup que le numérateur et le dénominateur ont la même "force" (alors qu'avant il y avait une puissance écrasant l'autre).
Lever l'indétermination pour des fractions rationnelles est souvent simple: c'est toujours la même astuce, on met en facteur la plus grande puissance possible et on observe. Mais ce n'est pas toujours très simple de lever une indéterimination par exemple pour des fractions irrationelles:
superieur/factorisation-racine-carree-pour-exo-sur-les-limites-t173449.html
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Mathématiques - Domaine d'une fonction.
ici il y a plus simple pour calculer les limites en l'infini
f(x) = (2x)/(4x^2) + 1/(4x^2)
calcule la limite de chaque terme ....
f(x) = (2x)/(4x^2) + 1/(4x^2)
calcule la limite de chaque terme ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
