Exercices algèbre
30 messages
- Page 2 sur 2 - 1, 2
Re: Exercices algèbre
Ben314, tu montres que ^{2^n}-1) est divisible par
est divisible par 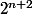 pour tout
pour tout  . Tout le monde en est d'accord. Mais ce n'est pas divisible par
. Tout le monde en est d'accord. Mais ce n'est pas divisible par  .
.
Re: Exercices algèbre
Si je comprends bien, il est impossible de résoudre l'exercice tel que je l'ai proposé.
Donc en essayant de le refaire avec ce que vous me proposez, je dois montrer que
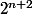 divise
divise^{2^{n}}-1)
Initialisation : n = 1
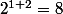
^{2} - 1 = 4k^{2}+4k)
-> Voyez comme mon niveau est bas, je n'arrive même pas à initialiser...
Ensuite pour l'hérédité je devrais supposer que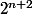 divise
divise^{2^{n}}-1) et montrer que
et montrer que  divise
divise^{2^{n+1}}-1)
Donc en essayant de le refaire avec ce que vous me proposez, je dois montrer que
Initialisation : n = 1
-> Voyez comme mon niveau est bas, je n'arrive même pas à initialiser...
Ensuite pour l'hérédité je devrais supposer que
Re: Exercices algèbre
Ben314 a écrit:car
ou
est pair (par contre
est impair lorsque
est congru à 1 ou 2 modulo 4)
Si ce n'est pas trop demandé, pourriez-vous ré-expiquer cette partie ?
Re: Exercices algèbre
Damien01 a écrit:
Initialisation : n = 1
Bonjour
Pour l'initialisation:
4k²+4k=4k(k+1)
L'un des nombres k et (k+1) est pair donc 4k²+4k est bien divisible par 8
Re: Exercices algèbre
Ah mais oui je suis bête ! Merci !
Par contre pour l'hérédité :
On suppose que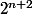 divise
divise ^{2^{n}}-1)
On souhaite montrer que divise
divise ^{2^{n+1}}-1)
J'arrive à montrer que
^{2^{n+1}}-1=[(2k+1)^{n}-1] [(2k+1)^{n}+1]) qui est divisible par
qui est divisible par 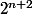 mais comment montrer que c'est divisible par
mais comment montrer que c'est divisible par  ?
?
Par contre pour l'hérédité :
On suppose que
On souhaite montrer que
J'arrive à montrer que
Re: Exercices algèbre
Ton identité est fausse. Corrige-là.
Une fois corrigé, l'hypothèse de récurrence donne tout de suite qu'un des facteurs est divisible par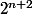 , et on en déduit que l'autre est pair.
, et on en déduit que l'autre est pair.
Une fois corrigé, l'hypothèse de récurrence donne tout de suite qu'un des facteurs est divisible par
Re: Exercices algèbre
Comment déduisez-vous que
Si j'ai bien compris, vous dites que
Re: Exercices algèbre
Damien01 a écrit:divise
Comment déduisez-vous queest impaire ???
Si j'ai bien compris, vous dites queest impaire donc
et
sont paires ? Ainsi on peut écrire
divisible par
???
Quand tu élèves un nombre impair à n'importe quelle puissance, tu obtiens un nombre impair.
le premier facteur est divisible par
le second facteur est divisible par 2 (nombre impair augmenté de 1)
Re: Exercices algèbre
D'accord ! Je viens seulement de comprendre...
Excusez-moi pour tout le dérangement, j'ai du en énerver plus d'un...
En tout cas merci à vous !
Excusez-moi pour tout le dérangement, j'ai du en énerver plus d'un...
En tout cas merci à vous !
30 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
