Tu peux faire quelque chose avec les nombres hypercomplexes; ça rentre dans les extension de corps, donc ça devrait aller;
On a R[i] avec i² = -1, qu'on connait bien, mais aussi:
R[e] avec

et

et aussi
R[f] avec

et

.
Tu as une interprétation géométrique sympa en dimension 2 en prenant les matrices
1=
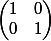
i=
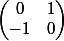
e=

et f=
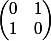
c'est à dire que tu retrouveras les similitudes directes, puis les "projections orthogonales" composées avec une homothéties et enfin les similitudes indirectes ce qui rendra ton exposé plus digeste.
Pour être plus complet, tu trouvera l'article de Luc Sinégre, qui enseigne en spé et est un ami,dans une publication de l'IREM de Rouen: Pourqoi aimer faire des maths au lycée (plein d'articles dont 2 de moi (François Prévost)).
Voici le lien:
[url]https://www.google.fr/search?q=Pourquoi+aimer+encore+les+maths+au+lycée,+IREM+de+Rouen&ie=utf-8&oe=utf-8&g[/url]
Bon courage.





 .
.
 .
.