Trouver des transformées de laplace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 27 Déc 2015, 00:53
par ilikoko123 » 27 Déc 2015, 00:53
Rik95 a écrit:On obtient donc im[(1/(i-p))*e^t(i-p)] de 3 a + l'infini si je ne me trompe pas ? Pour le calcul en 3 c'est facile mais en +infini je ne vois pas trop
la norme de ce qui est entre crochets ne contient qu'un
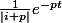
p>0 ...
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 27 Déc 2015, 01:35
par Rik95 » 27 Déc 2015, 01:35
Sake a écrit:Ben voilà. Et maintenant, quelle est la fonction que tu intègres ? Peux-tu m'écrire max(0, a - t) de manière implicite ?
Je dirai que Max(0, a-t) = a quand t = a
ilikoko123 a écrit:la norme de ce qui est entre crochets ne contient qu'un
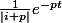
p>0 ...
Désolé mais je ne comprend pas pourquoi ... pour moi Im de l'integral de e^(-pt+it) = Im de l'integral de e^(t(p-i)) = [(1/(p-i))e^(t(p-i))

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 27 Déc 2015, 01:40
par Sake » 27 Déc 2015, 01:40
Rik95 a écrit:Je dirai que Max(0, a-t) = a quand t = a
Aïe aïe aïe... As-tu seulement fait un dessin comme je le répète depuis le début ?
Je suis d'accord que max(0,a-t) = 0 pour t >= a, mais qu'est-ce qui se passe avant ?
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 27 Déc 2015, 01:51
par Rik95 » 27 Déc 2015, 01:51
Sake a écrit:Aïe aïe aïe... As-tu seulement fait un dessin comme je le répète depuis le début ?
Je suis d'accord que max(0,a-t) = 0 pour t >= a, mais qu'est-ce qui se passe avant ?
Oui j'ai bien fait un dessin, je vois que le max est a quand t < a .., pour t = 0 on a, t=1 on a a-1, .. etc jusqu'a arriver a la valeur de a ou on aura 0

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 27 Déc 2015, 01:57
par Sake » 27 Déc 2015, 01:57
Rik95 a écrit:Oui j'ai bien fait un dessin, je vois que le max est a quand t < a .., pour t = 0 on a, t=1 on a a-1, .. etc jusqu'a arriver a la valeur de a ou on aura 0
Donc il est évident que max(0,a-t) = a-t pour t < a...
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 27 Déc 2015, 01:59
par Rik95 » 27 Déc 2015, 01:59
Sake a écrit:Donc il est évident que max(0,a-t) = a-t pour t < a...
Ah tu parles par apport a chaque point, dans ce cas oui je suis d'accord, je voyais par apport a tout l'intervalle entre 0 et a enfaîte ^^

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 27 Déc 2015, 09:10
par Sake » 27 Déc 2015, 09:10
Rik95 a écrit:Ah tu parles par apport a chaque point, dans ce cas oui je suis d'accord, je voyais par apport a tout l'intervalle entre 0 et a enfaîte ^^
Ben je vois pas par rapport à quoi d'autre on pourrait définir une fonction explicitement définie par t -> max(0,a-t) sur R+...
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 27 Déc 2015, 11:15
par Rik95 » 27 Déc 2015, 11:15
Sake a écrit:Ben je vois pas par rapport à quoi d'autre on pourrait définir une fonction explicitement définie par t -> max(0,a-t) sur R+...
Je vois ^^
Parcontre je ne comprend toujours pas comment tu as fais pour le reste, j'ai essayer de calculer la transformée de a-t cela me donne a/p - 1/p²

-
Sake
- Habitué(e)
- Messages: 1392
- Enregistré le: 17 Juil 2014, 21:32
-
 par Sake » 27 Déc 2015, 15:57
par Sake » 27 Déc 2015, 15:57
Rik95 a écrit:Je vois ^^
Parcontre je ne comprend toujours pas comment tu as fais pour le reste, j'ai essayer de calculer la transformée de a-t cela me donne a/p - 1/p²
Sur quel intervalle intègres-tu ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Déc 2015, 18:23
par Ben314 » 27 Déc 2015, 18:23
Une remarque : lorsque p=0 (ou tend vers 0),
(p))
, c'est l'intégrale de la fonction sur R+, donc la surface sous la courbe si la fonction est positive.
Là, la surface sous la courbe, c'est un demi carré de coté a donc de surface a²/2 et ton a/p-1/p², il ne tend pas vraiment vers a²/2 lorsque p tend vers 0...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 27 Déc 2015, 22:31
par Rik95 » 27 Déc 2015, 22:31
Jintègre de 0 à a, j'ai refais mes calculs mais je me trompe encore -_- :/, je trouve (-1/p²+p) + a/p + e^-ap((-a/p)+1/(p+1)) ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 27 Déc 2015, 23:04
par Ben314 » 27 Déc 2015, 23:04
J'arrive rien à lire de ce que tu écrit....
perso, je trouve

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 28 Déc 2015, 01:17
par Rik95 » 28 Déc 2015, 01:17
J'ai refais mes calculs plusieurs fois je ne trouve pas comme vous ><, peut etre que mes déduction sont fausse ?
Je commence par intégrer a*e^-p^t je trouve (-a/p)*e-(ap) + a/p
Ensuite je fais une integration par parties pour trouver l'integral de t*e^-pt je trouve que lintégral de t*^e-(pt)*((p+1)/p= - lintégral de e^-pt , de la je déduit lintégrale de te^-pt et je termine les calculs ... mais je ne trouve pas du tout la meme chose :/
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 28 Déc 2015, 19:53
par Rik95 » 28 Déc 2015, 19:53
-
ilikoko123
- Membre Relatif
- Messages: 219
- Enregistré le: 09 Oct 2015, 21:40
-
 par ilikoko123 » 28 Déc 2015, 20:48
par ilikoko123 » 28 Déc 2015, 20:48
ilikoko123 a écrit:la norme de ce qui est entre crochets est
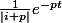
p>0 ...
es tu d'accord ?
-
Rik95
- Membre Relatif
- Messages: 211
- Enregistré le: 08 Oct 2014, 15:46
-
 par Rik95 » 28 Déc 2015, 21:30
par Rik95 » 28 Déc 2015, 21:30
ilikoko123 a écrit:es tu d'accord ?
Pas vraiment, je ne comprend pas comment tu es arriver a cette expression ?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 28 Déc 2015, 23:38
par aymanemaysae » 28 Déc 2015, 23:38
La méthode de M. ilikoko123 donne le même résultat:

t})
dt =

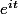

dt =

(cos(t) + i sin(t))

dt
=

cos(t)

dt + i

sin(t)

dt,
donc

sin(t)

dt = Im(

t})
dt) .

t})
dt =
t}}{i - p})
=

t})
= -


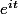
= -

(i + p)(cos(t) + i sin(t))
= -

(p cos(t) - sin(t) + i(cos(t) + p sin(t))),
donc

sin(t)

dt = Im(

t})
dt) = -

(cos(t) + p sin(t))),
donc
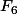
(p) =
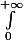
f(t) dt =

0 dt +

sin(t)

dt =
 + cos(t))]}_3^{+ \infty})
=

(sin(3) p + cos(3))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
p>0 ...
t
dt = -
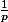
(- P
) t dt
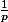
(
)' t dt = -
(
-
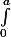
dt)
(
-
) = -
(a
+
-
) = -
,
(a - t)
dt =
=
.