Bonjour, je suis en L3 de maths, et en pleine révision pour les partiels ^^
J'aurai voulu savoir si quelqu'un pouvait m'éclairer sur un point.
Dans mon énoncé du théorème de fubini par exemple, on distingue 2 cas, celui ou ma fonction et à valeur dans [0,+(l'infini)] et celui ou ma fonction est à valeurs dans C. Dans celui ou la fonction est à valeur positive, le théorème ne signale pas qu'il faut vérifier que la fonction est intégrable par rapport à la mesure, alors que dans celui ou la fonction est à valeur dans C, on nous donne plusieurs équivalences par rapport au fait que les fonctions sont intégrables. J'aurai voulu savoir si quelqu'un pouvait m'expliquer cela ? De plus, cela voudrait-il dire que quand une fonction est à valeur dans [0,+(linfini)] signifie forcément que celle-ci est intégrable ?
Merci de vos réponses :)
Théorie de la mesure/intégration
4 messages
- Page 1 sur 1
Salut,
Tout dépend (évidement...) de la définition qu'on prend du terme "intégrable".
Lorsqu'une fonction mesurable est à valeur dans
est à valeur dans 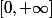 , on peut dans tout les cas donner un sens à l'intégrale de
, on peut dans tout les cas donner un sens à l'intégrale de  qui est à valeur dans
qui est à valeur dans 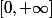 , mais a peu prés tout les auteurs s'entendent à dire qu'elle est intégrable uniquement si son intégrale est différente de +oo.
, mais a peu prés tout les auteurs s'entendent à dire qu'elle est intégrable uniquement si son intégrale est différente de +oo.
Pour de telles fonctions, la formule du théorème de Fubini est systématiquement valable avec évidement la possibilité que la formule en question dise que +oo=+oo.
Ensuite, dans le cas de fonctions à valeur dans R (ou C), si tu regarde la définition de l'intégrale au sens de Lebesgue, on se ramène au cas de fonction à valeur positives en écrivant que f=Max(f,0)-Max(-f,0) où les deux fonctions Max(0,f) et Max(0,-f) sont évidement à valeur positives.
On pose donc par définition-\int\text{Max}(-f,0)) et il est bien clair que, si les deux intégrales de Max(f,0) et Max(-f,0) sont infinies, on est dans la m... pour définir l'une moins l'autre. Donc pour pouvoir donner du sens à cette définition, on demande que les deux intégrales en question soient finies (et c'est la définition d'une fonction intégrable)
et il est bien clair que, si les deux intégrales de Max(f,0) et Max(-f,0) sont infinies, on est dans la m... pour définir l'une moins l'autre. Donc pour pouvoir donner du sens à cette définition, on demande que les deux intégrales en question soient finies (et c'est la définition d'une fonction intégrable)
Evidement pour démontrer la formule de Fubini dans ce cas, comme on va passer par cette définition pour prouver le résultat (après l'avoir prouvé pour les fonctions à valeur dans [0,+oo]) il faut que les fonctions soient intégrables.
EDIT : grilled...
Tout dépend (évidement...) de la définition qu'on prend du terme "intégrable".
Lorsqu'une fonction mesurable
Pour de telles fonctions, la formule du théorème de Fubini est systématiquement valable avec évidement la possibilité que la formule en question dise que +oo=+oo.
Ensuite, dans le cas de fonctions à valeur dans R (ou C), si tu regarde la définition de l'intégrale au sens de Lebesgue, on se ramène au cas de fonction à valeur positives en écrivant que f=Max(f,0)-Max(-f,0) où les deux fonctions Max(0,f) et Max(0,-f) sont évidement à valeur positives.
On pose donc par définition
Evidement pour démontrer la formule de Fubini dans ce cas, comme on va passer par cette définition pour prouver le résultat (après l'avoir prouvé pour les fonctions à valeur dans [0,+oo]) il faut que les fonctions soient intégrables.
EDIT : grilled...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
