Matrice diagonalisable

[mathelot]

bonjour,

pourriez m'indiquer plusieurs raisons pour lesquelles


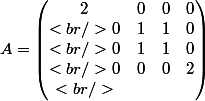
est diagonalisable.

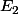
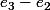
Pour l'instant, j'ai deux vecteurs propres dans et un vecteur dans le noyau

le polynôme caractéristique est
Merci.

[Skullkid]

Bonjour, plusieurs raisonnements "courts", c'est-à-dire sans chercher à effectuer la diagonalisation à la bourrin :

- A est symétrique rélle donc diagonalisable.
- On remarque, parce qu'on a du nez, que A^2 = 2A, donc A admet un annulateur scindé à racines simples, donc A est diagonalisable.
- On calcule le polynôme caractéristique de A puis on le "simplifie" en virant ses racines multiples pour obtenir X^2-2X, d'où l'envie pressante de calculer A^2-2A.
- A est diagonale par blocs donc on se ramène à l'étude de son seul bloc non trivial, dont on voit rapidement qu'il est diagonalisable.

[zygomatique]

salut

pour rajouter un autre argument ... et compléter la réponse précédente ....

si (a, b, c, d) est la base dans laquelle est écrite A

a et d sont vecteurs propres associés à la valeur propre 2

mais aussi b + c ...

or a, b + c, d) est libre donc le sous-espace propre associé à la valeur propre 2 est de dimension 3

[mathelot]

merci.................

[paquito]

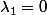
Les 2 valeurs propres de sont 0 et 2; Comme la multiplicité de est 1, le SEV propre de 0, le noyau est de dim1;

Pour
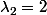
, on ne peut extraire de cette matrice aucun déterminant non nul d'ordre 2, 3 ou 4; par conséquent elle est de rang 1 et donc, son noyau qui est le SEV propre de est de dimension 3; elle est donc diagonalisable, son polynôme minimal est: et dans une base de vecteurs propres, elle s'écrit:
.