Dm équation 1ereS

[mangib]

:help: :help: :help: On considère l'équation suivante (E) d'inconnue x:
(m-1)x²-4mx+m-6=0 où m est un réel

1.on étudie le cas où m=1
Ecrire l'équation (E);puis la résoudre

2.on suppose désormais que m=/=1
déterminer m dans chacun des cas suivants(justifier vos réponses):
a) 1 est solution de (e)
b)(E) a une seule solution (indication (e) est donc équation du 2nd degré avec a=.., b=... et c=.. ayant un discriminant particulier)
c) (E) n'admet pas de solution réelle
d) Pour tout réel x, (m-1)x²-4mx+m-6<0


J'ai fait le 1. mais le 2. je ne comprend pas comment faut faire, j'ai essayé de faire le a) mais j'arrive à 12m²+28m+24 je ne devrais pas me retrouver avec des m² alors que je ne devrais pas en avoir
pouvez-vous m'aider, merci

[Carpate]

On considère l'équation suivante (E) d'inconnue x:
(m-1)x²-4mx+m-6=0 où m est un réel

1.on étudie le cas où m=1
Ecrire l'équation (E);puis la résoudre

2.on suppose désormais que m=/=1
déterminer m dans chacun des cas suivants(justifier vos réponses):
a) 1 est solution de (e)
b)(E) a une seule solution (indication (e) est donc équation du 2nd degré avec a=.., b=... et c=.. ayant un discriminant particulier)
c) (E) n'admet pas de solution réelle
d) Pour tout réel x, (m-1)x²-4mx+m-6<0


J'ai fait le 1. mais le 2. je ne comprend pas comment faut faire, j'ai essayé de faire le a) mais j'arrive à 12m²+28m+24 je ne devrais pas me retrouver avec des m² alors que je ne devrais pas en avoir
pouvez-vous m'aider, merci

Et pourquoi et disparaitraient parce que tu remplaces x par 1 dans l'équation (E) ?
On te demande de déterminer m tel que 1 est racine de (E) donc tu arrives à une équation du second degré en m qu'il te faut résoudre ...

[mangib]

Et pourquoi et disparaitraient parce que tu remplaces x par 1 dans l'équation (E) ?
On te demande de déterminer m tel que 1 est racine de (E) donc tu arrives à une équation du second degré en m qu'il te faut résoudre ...

J'ai résolu la question 1 quand m=1 et je trouve x=5/4 mais c'est la question 2 a) qui me pose problème quand m est différent de 1, je ne vois pas comment procéder.

J'ai vu des exemples similaires sur internet où il ne restait que m et un réel, les m2 se trouvaient annulés dans le calcul mais pas dans mon exercice

[mangib]

Personne pour m'aider?

Je suis bloquée depuis plusieurs jours là dessus

[Carpate]

J'ai résolu la question 1 quand m=1 et je trouve x=5/4 mais c'est la question 2 a) qui me pose problème quand m est différent de 1, je ne vois pas comment procéder.

J'ai vu des exemples similaires sur internet où il ne restait que m et un réel, les m2 se trouvaient annulés dans le calcul mais pas dans mon exercice

Ah! J''avais ma lu l'équation (E). Il n'y a pas de !
1 solution de (E) s'écrit :
soit

[mangib]

Ah mais là je comprends plus rien.

Moi je calculais delta b2-4ac avec a=m-1 b=-4m et c=m-6 ce n'est pas à ça qu'il faut faire?

[Carpate]

Ah mais là je comprends plus rien.

Moi je calculais delta b2-4ac avec a=m-1 b=-4m et c=m-6 ce n'est pas à ça qu'il faut faire?

1 est solution de (E) donc il n'a plus de ni de remplacés respectivement par et et donc pas d'équation du second degré en x mais une équation du premier degré en m ...

[mangib]

Ah oui ça y est j'ai compris merci

Pour la b) je dois bien calculer delta par contre non? puisqu'il n'y a qu'une solution.

[mangib]

Je suis toujours bloquée sur la question 2 b) avec un delta qui vaut 12m2+28m-24.

Que faire ensuite? :mur:

[Grimmys]

Salut,

Pour la b), oui, tu dois bien calculer .

Rappelle toi simplement ton cours : pour quelle(s) valeur(s) de le polynôme admet une seule racine ?

[mangib]

Pour delta =0 j'ai donc essayé de résoudre -b/2a mais je me retrouve avec 4m/(2m-2)
Je ne sais pas quoi en faire je suis perdue

[Grimmys]

C'est vrai qu'on se perd facilement... Je n'ai jamais eu ce genre d'exercice, et ça déboussole un peu, effectivement.

Mais là, il me semble que tu ne t'y prends pas de la bonne façon : on ne te demande pas de déterminer cette unique solution, mais de déterminer m. Ce n'est donc pas la même chose.
Tout ce que tu sais - ce que tu as déterminé, preuve qu'on avance - c'est que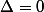 , que peux tu donc tenter de faire pour trouver m ?

Dans des exercices comme celui ci, avec différentes variables, formules possibles et résolutions, il faut vraiment voir le but dans sa tête ; ne pas tenter tout ce que l'on peut faire, mais uniquement ce qui peut être utile.
L'important là, est de comprendre qu'on ne cherche pas à résoudre l'équation, simplement déterminer la constante m.

Tu saisis ?

[mangib]

Oui j'avais bien compris qu'il fallait trouver m et donc je pensais calculer delta=o
MAIS je me retrouve avec 12m2+28m-24=0
Et là je bloque, je ne sais pas quoi utiliser pour trouver la valeur de m.
Je ne demande pas la réponse juste d'être aiguillée car je suis vraiment perdue.
Merci

[Grimmys]

Ah d'accord, pardon, mais je ne comprenais pas pourquoi tu calculais -b/2a.

La, je ne vois pas le soucis : Comme d'habitude, tu calcules le discriminant du polynome.

Dans le fond on calcule le discriminant d'un discriminant, c'est vrai que ça peut être un peu déroutant. ^^

[mangib]

Donc je recalcule delta c'est bien ça? J'y avait pensé mais je trouvais ça louche.

Merci de me confirmer

[Grimmys]

C'est tout à fait ça.

[matheudu83]

Tu peux me donner la résolution de l'équation (E) car si tu t'es tromper a ce stade , la suite sera fausse

[mangib]

J'ai trouvé m=-3 et m=2/3 avec delta =1936

[mangib]

Pour la c) (E) n'admet pas de solution, je comprend que delta doit être <0 je voit aussi que c'est pour toutes valeurs en dessous de zéro soit ]-oo;0] mais je ne voit pas comment le démontrer.

Merci de votre aide

[matheudu83]

remplace m par 1 puis resolue ton equation pour trouvez x , tu devrais trouvez 5/-4