Inégalités (valeur absolue)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
tem
- Messages: 6
- Enregistré le: 26 Sep 2006, 21:17
-
par tem » 26 Sep 2006, 21:33
Bonjour,
J'ai un DM à rendre dans les jours avenir et je bloque (complètement) sur quelques exercices. en fait, je ne vois pas comment partir ...
1.
\in\mathbb{R}^3, |a+b-c|\le |a|+|b|+|c|)
2. c'est fait,
[center]*****[/center]
3. Montrer que
\le 1+x^2)
4. En déduire (du 3) que
[center]*****[/center]
5. c'est fait,
6. c'est fait,
[center]*****[/center]
7.
\in (\mathbb{R},\mathbb{R}_+^*), |x|<\alpha, |\frac{1}{1+x^2}-1|< \alpha^2)
[center]*****[/center]
8. Soient
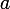
un nombre réel et
des nombres réels définis pour
par :
)
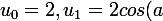, et,
Montrer que
)
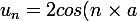[center]
Merci pour vos indications !![/center]
-
tem
- Messages: 6
- Enregistré le: 26 Sep 2006, 21:17
-
par tem » 26 Sep 2006, 21:49
Re -
Les quelques idées que j'ai :
1. C'est l'inégalité triangulaire :
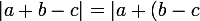|\le|a|+|b-c|)
Or :
Et donc :
Voila mon problème pour la première : je n'arrive pas à voir le lien ...
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
par Imod » 26 Sep 2006, 23:19
Il est vrai que donner un sujet par bribes en disant 1°) voilà la question , 2°) , 3°) je sais ... n'a pas de sens . Les questions d'un devoir s'enchaînent avec une certaine logique . L'ordre normal des choses est de donner le début du sujet jusqu'au point où l'on bloque pour demander quelque idées .
Imod
-
tem
- Messages: 6
- Enregistré le: 26 Sep 2006, 21:17
-
par tem » 26 Sep 2006, 23:36
Salut,
Bon, j'ai séparé les question si ca peut vous aider, mais les questions peuvent être résolus indépendemment (d'après la prof).
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
par Imod » 27 Sep 2006, 00:08
Ce n'est pas parce que les questions sont indépendantes que le sujet est un ramassis de résultats indépendants . Il faut connaître l'ensemble du sujet pour combler les vides .
Imod
-
tem
- Messages: 6
- Enregistré le: 26 Sep 2006, 21:17
-
par tem » 27 Sep 2006, 00:37
allez des ptites idées svp
J'ai une idéee pour 7,
On a:
*Pour
<br />\\<br />\alpha^2>x^2 \qquad (2)<br />\\<br />(1)\times (2) = \alpha^2(1+x^2)>x^2 \Rightarrow |\frac{1}{x^2+1}-1|0 \Rightarrow |\frac{1}{x^2+1}-1|<\alpha^2)
Donc
\in (\mathbb{R}, \mathbb{R^}_+^*),|\frac{1}{x^2+1}-1|<\alpha^2)
-
oss007
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Sep 2006, 09:39
-
par oss007 » 27 Sep 2006, 04:58
pour le 1) : a+b-c= a+b+(-c) puis inégalité triangulaire
-
tem
- Messages: 6
- Enregistré le: 26 Sep 2006, 21:17
-
par tem » 27 Sep 2006, 05:46
Pour l'inégalité triangulaire j'ai fait ca :
Est ce que c'est bon aussi,
et svp vérifier l'exercice 7 également.
[CENTER]
[/CENTER]
Avec votre methode oss007 :
|\le|a+b|+|-c|)
or :
et
Donc
[CENTER]Donc :
\in \mathbb{R}^3, |a+b-c|\le|a|+|b|+|c|)
[/CENTER]
-
tem
- Messages: 6
- Enregistré le: 26 Sep 2006, 21:17
-
par tem » 27 Sep 2006, 19:58
Est -ce que c'est bon ?
-
oss007
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Sep 2006, 09:39
-
par oss007 » 28 Sep 2006, 04:21
oui , c'est bien ça.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
par abcd22 » 28 Sep 2006, 07:26
Bonjour,
tem a écrit:Or :
L'inégalité triangulaire, c'est
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
par allomomo » 01 Oct 2006, 17:35
Salut,
Pour le 3/7 : il faut distinguer des cas. (voire des intervalles)
Pour l'exercice 6, tu peux le faire avec les complexes ou bien avec la récurrence.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
