Argument d'un nombre complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par marius firmin » 22 Sep 2015, 11:28
par marius firmin » 22 Sep 2015, 11:28
Bonjour ,
Svp j'ai un probleme :
Sachant que "A" est l'argument du nombre complexe Z.
On demande d'exprimer
l'argument du nombre complexe :
( 2 + Z)/2i en fonction de "A" .
J'ai essayé d'appliquer la
formule de l'argument du rapport de
2 nombres complexes , mais je suis callé au moment d'exprimer l'argument de ( 2+Z).
Si quelqu'un peut me venir en aide ça m'arrengerai . merçi d'avance.
-
Robot
 par Robot » 22 Sep 2015, 11:43
par Robot » 22 Sep 2015, 11:43
L'argument de 2+Z ne dépend pas seulement de l'argument de Z, mais aussi de son module.

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 22 Sep 2015, 17:59
par chombier » 22 Sep 2015, 17:59
Robot a écrit:L'argument de 2+Z ne dépend pas seulement de l'argument de Z, mais aussi de son module.
Tout à fait, donc ton problème n'a pas de solutions.
En passant on ne dit pas "l'argument de Z" mais "un argument de Z"
-
Robot
 par Robot » 22 Sep 2015, 19:03
par Robot » 22 Sep 2015, 19:03
Ca dépend, Chombier, l'argument peut être un élément bien déterminé de
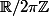
(un angle, quoi).

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 22 Sep 2015, 19:10
par chombier » 22 Sep 2015, 19:10
Robot a écrit:Ca dépend, Chombier, l'argument peut être un élément bien déterminé de
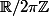
(un angle, quoi).
Encore un sous groupes de (R, +), je les oublie tout le temps
Pour moi un groupe, c'est noble, c'est dénombrable, voire, encore mieux, fini. Et pour moi R n'est pas un groupe, c'est un corps, je trouve ça très dévalorisant pour R de le considérer comme un groupe, c'est comme si on l'avait déclassé
-
Robot
 par Robot » 22 Sep 2015, 19:23
par Robot » 22 Sep 2015, 19:23

n'est pas un sous-groupe de

, mais un quotient de

, isomorphe au groupe des angles.

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 22 Sep 2015, 19:28
par chombier » 22 Sep 2015, 19:28
Robot a écrit:
n'est pas un sous-groupe de

, mais un quotient de

, isomorphe au groupe des angles.
Oui, c'est
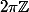
le sous groupe de

. Je m'exprime mal

 par marius firmin » 22 Sep 2015, 22:54
par marius firmin » 22 Sep 2015, 22:54
Ah pardon vous avez raison !
On a dit que r etait le module de Z
mais jusque là je ne vois pas
vraiment comment je peut exprimer
un argument de (2+Z) en fonction
de r et de A .
-
Robot
 par Robot » 23 Sep 2015, 08:06
par Robot » 23 Sep 2015, 08:06
marius firmin a écrit:Ah pardon vous avez raison !
On a dit que r etait le module de Z
mais jusque là je ne vois pas
vraiment comment je peut exprimer
un argument de (2+Z) en fonction
de r et de A .
Calcule
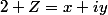
. Alors l'argument de

est

, pourvu que

ne soit pas un réel inférieur ou égal à
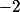
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
(un angle, quoi).
