Application lineaire AIDEZ MOI S'IL VOUS PLAIT

[never give up]

Je dois passer un concours et je suis tombee sur cet exercise que je n'est pas la solution :mur: :triste: AIDEZ MOI S'IL VOUS PLAIT

Soit la matrice A=(1 0 1 )
-1 2 1
-1 1 3

1 Comment déterminer l'application linéaire f (R^3,+,.) vers (R^3,+,.) qui a pour matrice A dans la base canonique B.
2 determinez ker f et precisez sa dimension
3 determinez im f et precisez sa dimension
4 determinez le rang de f

merci beaucoup :we:

[alphamethyste]

bonjour camarade

pour la premiere

Soit la matrice A=(1 0 1 )
-1 2 1
-1 1 3

1 Comment déterminer l'application linéaire f (R^3,+,.) vers (R^3,+,.) qui a pour matrice A dans la
base canonique B

[alphamethyste]

puis ensuite pour la deuxième

2 determinez ker f et precisez sa dimension

dans un premier temps on te demande le noyau Ker f

c'est à dire l'ensemble des vecteurs V de R^3 de l'ensemble de depart E=R^3 le R-espace vectoriel R^3 tels que quelque soit un element de E on vérifie

est l'élément neutre de l'ensemble d'arrivée c'est à dire en fait le R-espace vectoriel R^3

or on a vu que



donc le systeme à résoudre

x+z=0
-x+2y+z=0
-x+y+3z=0

tous les vecteurs de coordonnées (x,y,z) définis sur la base canonique et qui vérifient ce système sont les éléments de ker f

[capitaine nuggets]

Je dois passer un concours et je suis tombee sur cet exercise que je n'est pas la solution :mur: :triste: AIDEZ MOI S'IL VOUS PLAIT

Soit la matrice A=(1 0 1 )
-1 2 1
-1 1 3

1 Comment déterminer l'application linéaire f (R^3,+,.) vers (R^3,+,.) qui a pour matrice A dans la base canonique B.
2 determinez ker f et precisez sa dimension
3 determinez im f et precisez sa dimension
4 determinez le rang de f

merci beaucoup :we:

Salut !

2. Considère le système d'inconnues :

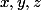
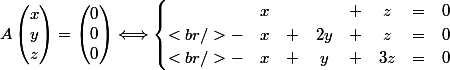
[CENTER][/CENTER]

A l'aide de la méthode de Gauss, montre que ce système équivaut à :

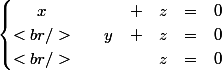
[CENTER] [/CENTER]

Trouver le noyau revient à résoudre le système précédent.

3. Pour trouver l'image il suffira de remarquer que est injectif et le tour est joué :+++:

4. Par définition .

:+++:

[alphamethyste]

lollll :dodo:

tu as terminé avant moi Captain Nuggets ,

bon je retourne à l'autre topic , merci camarade!