Argument et lieux géométriques avec les nombres complexes
20 messages
- Page 1 sur 1
argument et lieux géométriques avec les nombres complexes
Si possible de m expliquer les points suivants sur les nombres complexes
1) Est-ce que je dois utiliser l argument dit principale ou argument d un nombre complexe
Par exemple
arg(-i)= -pi/2 mod[2pi] ou bien arg(-i)= 3pi/2 mod[2pi]
arg(-1/2-racine(3)/2 *i)=4pi/3 ou arg(-1/2-racine(3)/2 *i)=-2pi/3 mod[2pi]
est ce que je doit travailler sur ]-pi,+pi] ou [0,2pi[
2) une question concernant les lieux géométriques avec les nombres complexes
Mon problème c est aux niveaux de limiter un lieu ( les points a éliminer ou limites )
Z=z-zB/z-zA M(z) A(zA) et B(zB)
Le travail avec les arguments et modulo 2pi
Chercher l ensemble des points M
1er cas Z est réel
Z est réel équivaut arg Z=o mod 2pi ou arg Z=pi mod 2pi
2em cas Z est imaginaire
Z est réel équivaut arg Z=pi/2 mod 2pi ou arg Z=3pi/2 mode 2pi
comment le traiter avec la méthode analytiques
Merci
1) Est-ce que je dois utiliser l argument dit principale ou argument d un nombre complexe
Par exemple
arg(-i)= -pi/2 mod[2pi] ou bien arg(-i)= 3pi/2 mod[2pi]
arg(-1/2-racine(3)/2 *i)=4pi/3 ou arg(-1/2-racine(3)/2 *i)=-2pi/3 mod[2pi]
est ce que je doit travailler sur ]-pi,+pi] ou [0,2pi[
2) une question concernant les lieux géométriques avec les nombres complexes
Mon problème c est aux niveaux de limiter un lieu ( les points a éliminer ou limites )
Z=z-zB/z-zA M(z) A(zA) et B(zB)
Le travail avec les arguments et modulo 2pi
Chercher l ensemble des points M
1er cas Z est réel
Z est réel équivaut arg Z=o mod 2pi ou arg Z=pi mod 2pi
2em cas Z est imaginaire
Z est réel équivaut arg Z=pi/2 mod 2pi ou arg Z=3pi/2 mode 2pi
comment le traiter avec la méthode analytiques
Merci
salut
connaissant un argument tu choisis celui que tu veux .... sauf mention spéciale dans l'énoncé ....
2/ utiliser toujours l'interprétation géométrique .... et vérifier les cas particuliers (du genre M = A ou M = B) ...
Z = (z - b)/(z - a) implique par exemple que z <> a !!!!
Z est réel <=> les vecteurs MA et MB sont colinéaires ....
Z est imaginaire pur <=> l'angle orienté (MA, MB) = pi/2 [2pi]
...
connaissant un argument tu choisis celui que tu veux .... sauf mention spéciale dans l'énoncé ....
2/ utiliser toujours l'interprétation géométrique .... et vérifier les cas particuliers (du genre M = A ou M = B) ...
Z = (z - b)/(z - a) implique par exemple que z <> a !!!!
Z est réel <=> les vecteurs MA et MB sont colinéaires ....
Z est imaginaire pur <=> l'angle orienté (MA, MB) = pi/2 [2pi]
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
salut zygomatique
merci pour votre aide
si possible de m expliquer d avantage les points suivants sur un exemple car les points qu il faut éliminer me pose un problème , remarque on travail avec modulo 2pi et non pi
1) pourquoi en utilise toujours la mesure principale pour les argument
((connaissant un argument tu choisis celui que tu veux .... sauf mention spéciale dans l'énoncé ....))
2/ utiliser toujours l'interprétation géométrique .... et vérifier les cas particuliers (du genre M = A ou M = B) ...
Z = (z - b)/(z - a) implique par exemple que z <> a !!!!
a) les vecteurs peuvent etres colinéaires de même sens ou de sens contraire
donc arg Z=0mod 2pi ou arg Z=pi mod 2pi
pour etudier Z est réel <=> Z=0 ou arg Z=0 mod 2pi ou arg Z=pi mod 2pi
Z est réel <=> les vecteurs MA et MB sont colinéaires ....
Z est imaginaire pur <=> Z=0o u l'angle orienté (MA, MB) = pi/2 [2pi] ou 'angle orienté (MA, MB) = -pi/2 [2pi]
svp expliquer la méthode sur l exemple suivant surtout au niveau des cas particuliers
par exemple Z=z-2i/z+3i
merci
merci pour votre aide
si possible de m expliquer d avantage les points suivants sur un exemple car les points qu il faut éliminer me pose un problème , remarque on travail avec modulo 2pi et non pi
1) pourquoi en utilise toujours la mesure principale pour les argument
((connaissant un argument tu choisis celui que tu veux .... sauf mention spéciale dans l'énoncé ....))
2/ utiliser toujours l'interprétation géométrique .... et vérifier les cas particuliers (du genre M = A ou M = B) ...
Z = (z - b)/(z - a) implique par exemple que z <> a !!!!
a) les vecteurs peuvent etres colinéaires de même sens ou de sens contraire
donc arg Z=0mod 2pi ou arg Z=pi mod 2pi
pour etudier Z est réel <=> Z=0 ou arg Z=0 mod 2pi ou arg Z=pi mod 2pi
Z est réel <=> les vecteurs MA et MB sont colinéaires ....
Z est imaginaire pur <=> Z=0o u l'angle orienté (MA, MB) = pi/2 [2pi] ou 'angle orienté (MA, MB) = -pi/2 [2pi]
svp expliquer la méthode sur l exemple suivant surtout au niveau des cas particuliers
par exemple Z=z-2i/z+3i
merci
plus d explications
salut cher zygomatique
svp donner moi plus d explications et une réponse complète
1/ on choisit celui qui nous convient ??? c e n est pas clair
2/ dans notre programme en utilise seulement mod (2pi)
donc comment répondre
Z = (z - 2i)/(z + 3i)
considérer B(2i) et A (-3i)
argZ il faut Z non nul donc ZB différent de 0
Z existe ssi ZA diffèrent de 0
merci beaucoup
svp donner moi plus d explications et une réponse complète
1/ on choisit celui qui nous convient ??? c e n est pas clair
2/ dans notre programme en utilise seulement mod (2pi)
donc comment répondre
Z = (z - 2i)/(z + 3i)
considérer B(2i) et A (-3i)
argZ il faut Z non nul donc ZB différent de 0
Z existe ssi ZA diffèrent de 0
merci beaucoup
salut mathelot
merci pour votre aide
voici mon problème exactement :
1er pb) est ce que je dois prendre a chaque fois la mesure principale ou non pour déterminer l argument
2em pb)
dans mon programme en utilise les modulo 2pi
comment utiliser les arguments pour déterminer un ensemble de point et surtout comment enlever les points limites
soient M(z) A(zA) B(zB)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
les conditions a remplir pour limiter l ensemble des points ?
merci
merci pour votre aide
voici mon problème exactement :
1er pb) est ce que je dois prendre a chaque fois la mesure principale ou non pour déterminer l argument
2em pb)
dans mon programme en utilise les modulo 2pi
comment utiliser les arguments pour déterminer un ensemble de point et surtout comment enlever les points limites
soient M(z) A(zA) B(zB)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
les conditions a remplir pour limiter l ensemble des points ?
merci
georgets555 a écrit:salut mathelot
merci pour votre aide
voici mon problème exactement :
1er pb) est ce que je dois prendre a chaque fois la mesure principale ou non pour déterminer l argument
considérer la mesure principale d'un angle, c'est aller contre le modulo (tous les résidus
sont équivalents), c'est détruire la classe d'équivalence. Donc considérer
la mesure principale uniquement quand c'est demandé dans l'énoncé.
2em pb)
dans mon programme en utilise les modulo 2pi
comment utiliser les arguments pour déterminer un ensemble de point et surtout comment enlever les points limites
Les droites, demi droites ou droites épointées
sont déterminées par un angle constant avec l'horizontal.
soient M(z) A(zA) B(zB)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
les conditions a remplir pour limiter l ensemble des points ?
merci
.........................................
une réponse
salut mathelot
1er)
je n est pas compris (considérer la mesure principale d'un angle, c'est aller contre le modulo (tous les résidus
sont équivalents), c'est détruire la classe d'équivalence.) donner moi plus d explications et un exemple concret
2em)
donner moi une réponse
pour cette question car mon problème au niveau des points a éliminer de l ensemble
soient M(z) A(2i) B(i)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
merci bien
1er)
je n est pas compris (considérer la mesure principale d'un angle, c'est aller contre le modulo (tous les résidus
sont équivalents), c'est détruire la classe d'équivalence.) donner moi plus d explications et un exemple concret
2em)
donner moi une réponse
pour cette question car mon problème au niveau des points a éliminer de l ensemble
soient M(z) A(2i) B(i)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
merci bien
la congruence est une classe d'équivalence. Tous les résidus jouent le même rôle
à l'intérieur d'une classe. Faire le choix d'un élément casse cette équivalence.
Un intérêt de choisir un élément dans une classe d'équivalence peut se voir:
- quand on veut des vecteurs d'origine O (plan vectoriel=plan affine pointé)
ou quand on construit des fonctions non mesurables en choisissant, via l'axiome du choix,
un élément dans chaque classe. Mais pour les mesures d'angle, c'est inutile de particulariser
un éléments parmi ses congénères :)
à l'intérieur d'une classe. Faire le choix d'un élément casse cette équivalence.
Un intérêt de choisir un élément dans une classe d'équivalence peut se voir:
- quand on veut des vecteurs d'origine O (plan vectoriel=plan affine pointé)
ou quand on construit des fonctions non mesurables en choisissant, via l'axiome du choix,
un élément dans chaque classe. Mais pour les mesures d'angle, c'est inutile de particulariser
un éléments parmi ses congénères :)
ensemble à déterminer
salut mathelot
merci pour les explications
donner moi une réponse svp
pour cette question car mon problème au niveau des points a éliminer de l ensemble
soient M(z) A(2i) B(i)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
merci bien
merci pour les explications
donner moi une réponse svp
pour cette question car mon problème au niveau des points a éliminer de l ensemble
soient M(z) A(2i) B(i)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
merci bien
georgets555 a écrit:salut mathelot
merci pour les explications
donner moi une réponse svp
pour cette question car mon problème au niveau des points a éliminer de l ensemble
soient M(z) A(2i) B(i)
Z= (z-zB)/(zM-zA)
1) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
2) déterminer l ensemble des points tel que Z soit réel en utilisant les arguments modulo 2pi
merci bien
ça ne serait pas
est ce que il faut le démontrer le résultat
salut mathelot
est ce que il faut le démontrer le résultat
(AB) privé du point A tu n as pas utiliser les arguments ?
2) déterminer l ensemble des points tel que Z soit imaginaire en utilisant les arguments modulo 2pi
merci
est ce que il faut le démontrer le résultat
(AB) privé du point A tu n as pas utiliser les arguments ?
2) déterminer l ensemble des points tel que Z soit imaginaire en utilisant les arguments modulo 2pi
merci
équation droite (AB) en complexes
le quotient
 est le quotient de proportionnalité entre les vecteurs
est le quotient de proportionnalité entre les vecteurs
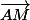 et
et 
Pour signifier que la droite (AB) est "maigre" - c'est une R-droite mais pas une C-droite -
on dit que ce coefficient de proportionnalité est réel, ce qui assure la maigreur de ladite droite

soit
(\bar{z_B}-\bar{z_A})-(z_B-z_A)(\bar{z}-\bar{z_A})=0)
-\bar{z}(z_B-z_A)-z_A(\bar{z_B}-\bar{z_A})+\bar{z_A}(z_B-z_A)=0)
en posant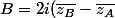) et
et 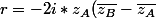+2i \bar{z_A}(z_B-z_A))
on obtient finalement
 où
où 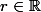
qui est l'équation générique d'une droite en complexe
Pour signifier que la droite (AB) est "maigre" - c'est une R-droite mais pas une C-droite -
on dit que ce coefficient de proportionnalité est réel, ce qui assure la maigreur de ladite droite
soit
en posant
on obtient finalement
qui est l'équation générique d'une droite en complexe
avec les arguments
salut mathelot
merci pour votre réponse
mais comment traiter la question
en utilisant les arguments ,en transforme le quotient avec des angles orientés modulo 2pi
comment déterminer l ensembles des points tels que zM-zB/zM-zA pour qu il soit réel ou bien imaginaire
merci
merci pour votre réponse
mais comment traiter la question
en utilisant les arguments ,en transforme le quotient avec des angles orientés modulo 2pi
comment déterminer l ensembles des points tels que zM-zB/zM-zA pour qu il soit réel ou bien imaginaire
merci
autre façon pour répondre
salut mathelo
merci pour votre réponse
pardonner je crois qu il y a une faute de notation au niveau du rapport
voici l écriture juste du rapport
le rapport s écrit Z=zM-zA /zM-zB ou A(zA), B(zB) et M(zM)
d ou l expression de votre droite doit changer
svp
comment répondre en utilisant les arguments
merci
merci pour votre réponse
pardonner je crois qu il y a une faute de notation au niveau du rapport
voici l écriture juste du rapport
le rapport s écrit Z=zM-zA /zM-zB ou A(zA), B(zB) et M(zM)
d ou l expression de votre droite doit changer
svp
comment répondre en utilisant les arguments
merci
merci pour tes conseils
salut mathelot
merci pour tes conseils et tes réponses
il y a une faute au niveau du rapport utiliser donc votre calcul sera faux
mais svp
donner moi une réponse avec les arguments
merci beaucoup
merci pour tes conseils et tes réponses
il y a une faute au niveau du rapport utiliser donc votre calcul sera faux
mais svp
donner moi une réponse avec les arguments
merci beaucoup
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
