Théorème de Moivre-Laplace

par **mathelot** » 12 Juin 2015, 15:30

bonjour,
le thm de Moivre-Laplace enseigné en Terminale
semble être une conséquence du théorème central limite.
Je ne vois pas quelles hypothèse prendre, dans quel cadre se situer précisemment,
pour découler Moivre-Laplace du théorème central limite.

dans le TCL , il s'agit de n variables de même loi, avec EX et sigma(X) constantes
et dans Moivre Laplace de n v.a de loi binomiale dépendant de n.

quelque chose m'échappe.

merci.

par **zygomatique** » 12 Juin 2015, 15:54

salut

n'est-ce pas n v.a. de Bernoulli ?

X_n est la somme de n v.a. de Bernoulli de paramètres p qui sont indépendantes donc X_n suit la loi binomiale B(n, p)

par **Matt_01** » 12 Juin 2015, 16:10

Il faut appliquer le TCL à la suite des variables aléatoires X1, ... de loi B(1,p) pour obtenir de Moivre Laplace.

par **DamX** » 12 Juin 2015, 16:23

wow on fait ça en term maintenant ? :doh:
Les 3/4 ont du mal à dériver un polynôme ou faire une IPP et on leur montre une convergence en loi ? Ca doit être sacrément édulcoré..

par **zygomatique** » 12 Juin 2015, 16:55

on ne leur montre pas !!! on leur dit que .... !!!!

par **mathelot** » 15 Juin 2015, 08:47

autre question:

que prend on en terminale comme intervalle de confiance
de la proportion du caractère

où

X_i v.a de Bernoulli

est ce que l'on majore

par 1, ou on cherche
à estimer p par M_n

par **zygomatique** » 15 Juin 2015, 09:57

en seconde "ça" vaut 1 ...

en term sti on ne travaille qu'avec des intervalles à 95% donc u_a = 1,96

en TS on détermine le u_a correspondant au seuil a ...

mais attention à ne pas confondre intervalle de confiance et intervalle de fluctuation

p est connue =>

au niveau de confiance 1 - a ou au seuil de risque a

p est inconnue et f est le résultat d'un échantillon de taille n =>

au niveau de confiance 1- a ou au seuil de risque a

dans le dernier cas on corrige parfois l'écart type en remplaçant n par n - 1 (du fait du biais introduit dans le calcul de la variance)

par **mathelot** » 16 Juin 2015, 08:45

je ne comprends pas ton

pour l'intervalle de confiance ?
dans le Nathan de terminale "Hyperbole", ils donnent cette même formule sans explication.

par **mathelot** » 16 Juin 2015, 15:20

mathelot a écrit:je ne comprends pas ton pour l'intervalle de confiance ?
dans le Nathan de terminale "Hyperbole", ils donnent cette même formule sans explication.

up.................

par **zygomatique** » 16 Juin 2015, 16:18

l'intervalle de confiance signifie qu'on veut estimer la proportion théorique p inconnue .... avec la fréquence f obtenue à partir d'un échantillon ....

mais lorsque on estime une proportion on sait que l'écart type est donnée par la formule R(p(1 - p)) or on ne connaît pas p et il nous faut un écart type .... qu'on estime à partir de f ....

par **mathelot** » 16 Juin 2015, 18:02

j'ai lu que la variance empirique présente un biais.

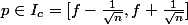
zygomatique a écrit:p est inconnue et f est le résultat d'un échantillon de taille n => au niveau de confiance 1- a ou au seuil de risque a

dans le dernier cas on corrige parfois l'écart type en remplaçant n par n - 1 (du fait du biais introduit dans le calcul de la variance)

est ce une formule enseignée en Terminale ?

ou est-ce:

par **zygomatique** » 16 Juin 2015, 18:24

il y a des exercices dans les chapitres concernés ...

on voit le dernier dès la seconde ....

par **muse** » 17 Juin 2015, 18:56

mathelot a écrit:j'ai lu que la variance empirique présente un biais.

est ce une formule enseignée en Terminale ?

ou est-ce:

D'ailleurs j'avais ouvert ce sujet:
http://www.maths-forum.com/intervalle-fluctuation-confiance-165808.php

Il y a dedans un article très intéressant de Daniel Perrin.

Si au passage tu as la réponse à ma question

Théorème de Moivre-Laplace

théorème de Moivre-Laplace

Qui est en ligne