Chiffre des unites

[adamNIDO]

Bonjour,

votre aide svp

[Axiom]

Quelque chose de très classique en informatique, il peut-être obtenu par l'algorithme suivant, ici, écrit en java :

public static void main(String[] args) {

double a = Math.pow(3, 125);
int dizaine = (int) a/10; // Nombre des dizaines arrondi
int unite = (int) a - dizaine*10; // Obtention du chiffre unité

System.out.println("Le chiffre des unités est : "+unite);


}

Le résultat ici est 7. :lol3:

[mathelot]

bjr,

le chiffre des unités d'un entier est son résidu modulo 10.







l'exposant est donc à traiter modulo 4


le chiffre des unités de est le même que le chiffre des unités de : 3.

[adamNIDO]

Quelque chose de très classique en informatique, il peut-être obtenu par l'algorithme suivant, ici, écrit en java :

public static void main(String[] args) {

double a = Math.pow(3, 125);
int dizaine = (int) a/10; // Nombre des dizaines arrondi
int unite = (int) a - dizaine*10; // Obtention du chiffre unité

System.out.println("Le chiffre des unités est : "+unite);


}

Le résultat ici est 7. :lol3:

est ce que tu peux m'explique algorithme mathématiquement
est ce que tu peux le refaire en c++ sous forme de exe merci d'avance

[adamNIDO]

bjr,

le chiffre des unités d'un entier est son résidu modulo 10.







l'exposant est donc à traiter modulo 4


le chiffre des unités de est le même que le chiffre des unités de : 3.

merci mais est ce ue tu peux m'explique avec a et b tel que

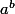
[chombier]

Quelque chose de très classique en informatique, il peut-être obtenu par l'algorithme suivant, ici, écrit en java :

public static void main(String[] args) {

double a = Math.pow(3, 125);
int dizaine = (int) a/10; // Nombre des dizaines arrondi
int unite = (int) a - dizaine*10; // Obtention du chiffre unité

System.out.println("Le chiffre des unités est : "+unite);


}

Le résultat ici est 7. :lol3:

Ca ne fonctionne pas car le type double n'est pas assez grand pour que le résultat soit exact.
Ici a= 4.3667350287920675E59.

La conversion en int est encore pire, quelque part, un entier est codé sur 32 bits et ne peut pas du tout représenter un nombre aussi grand. Du coup java te renvoie le plus grand entier qu'il est capable de mettre dans le type int : 2147483647 = 2^31-1

Il faut travailler en scheme !!

>(expt 3 125)
436673502879206784130402698570834024654748577491697818855443

EDIT : je ne sais pas pourquoi le forum ajoute une espace au milieu de mon (grand) chiffre

[Axiom]

Oui, pardon, j'ai un peu merdouillé... ^^' :marteau:

[chombier]

Oui, pardon, j'ai un peu merdouillé... ^^' :marteau:

En java, pour les très grand nombres entiers, il faut utiliser la librairie BigInteger

[Axiom]

Oui, pardon, j'ai un peu merdouillé... ^^' :marteau:

La conversion en int était une grossière erreur de ma part, mais j'ai appris des choses comme ça.. Merci pour vos indications.
Et en C++ par contre, la mantisse des long n'est pas suffisante non plus, vous savez si il existe une librairie spéciale aussi ?

[chombier]

La conversion en int était une grossière erreur de ma part, mais j'ai appris des choses comme ça.. Merci pour vos indications.
Et en C++ par contre, la mantisse des long n'est pas suffisante non plus, vous savez si il existe une librairie spéciale aussi ?

C'est de ses erreurs qu'on apprend le plus !

EDIT : Il doit y avoir beaucoup de librairies en C++ qui proposent ça, vu la popularité du langage.
Je n'en sais pas plus, je n'aime pas beaucoup le C++.

Par contre je propose un algo qui marche avec des petits entiers :

Code: Tout sélectionner

#include

int main(int argc, char *argv[])
{
    int a = 1, i;

    for (i=0 ; i<125 ; i++)
        a = (a * 3) % 100000;
       
    printf("%d\n", a);
    return 0;
}

Il renvoie : 55443, soit les 5 derniers chiffres de 3^125

[mathelot]

merci mais est ce que tu peux m'explique avec a et b tel que

on effectue la division euclidienne de 125 par 4

[adamNIDO]

on effectue la division euclidienne de 125 par 4

oui mais svp quelle la regle que vous avez utilise pour dire que :

d'apres et que chiffre unites de est

[chombier]

on effectue la division euclidienne de 125 par 4

J'ai fait presque pareil



on effectue la division euclidienne de 125 par 2

[chombier]

oui mais svp quelle la regle que vous avez utilise pour dire que :

d'apres et que chiffre unites de est

Si tu ne connais pas ces règles, il te faut un petit cours d'arithmétique. Ou une autre méthode.

Est-ce que tu connais la notation ?

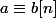
Sinon, l'autre méthode :
3^0 = 1
3^1 = 3
3^2 = 9
3^3 = 27
3^4 = 81
3^5 = 243
3^6 = 729
3^7 = 2187

On voit que le chiffre des unités est cyclique : 1, 3, 9, 7, 1, 3, 9, 7...

C'est même assez facile à démontrer.

Il faut alors chercher le 125ème terme de cette suite (le premier "1" de la suite étant le zero-ième terme)

[mathelot]

est une conséquence de


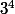
est élément neutre 1 pour la multiplication modulo 10,
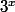
on peut donc réduire l'exposant x de modulo 4

[adamNIDO]

merci pour vous

j'ai deja lu le cours d'algorithme et je sais utiliser la notation de congruence mais juste je pense comment je peux faire ca sans calculatrice

[adamNIDO]

est une conséquence de


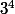
est élément neutre 1 pour la multiplication modulo 10,
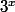
on peut donc réduire l'exposant x de modulo 4

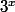
donc on peut dire que pour n'importe quelle l'exposant x de ona :

[adamNIDO]

J'ai fait presque pareil



on effectue la division euclidienne de 125 par 2

merci beaucoup

[chan79]

rien de nouveau mais on peut écrire

qui finit par 1

donc finit par 3

[adamNIDO]

rien de nouveau mais on peut écrire

qui finit par 1

donc finit par 3

pouvez vous me rappeller la regèle que vous avez utilise