Racines unités

par **yos** » 27 Jan 2010, 17:09

barbu23 a écrit:Ces corps intermediares entre et sont - ils donc de la forme

Etrange égalité entre un groupe et une extension de corps...

Même si p est premier c'est faux. Reprends ce que je dis dans le message 17.

par **yos** » 27 Jan 2010, 17:14

Regarde l'exo 3 de http://people.math.jussieu.fr/~keller/mt401/corr0902.pdf

par **barbu23** » 27 Jan 2010, 17:15

yos a écrit:Non : Z/nZ* est pas cyclique en général.
Quant aux sous-corps de , il en existe beaucoup d'autres (toujours en général). Par exemple contient comme sous corps .

Quel sont les sous groupes du groupe cyclique

, avec

premier ? :happy3:

par **Doraki** » 27 Jan 2010, 17:20

Quels sont les sous-groupes d'un groupe cyclique (Z/nZ) ?

par **yos** » 27 Jan 2010, 17:20

donc les sous-groupes de Z/pZ* sont les préimages des dZ/(p-1)Z où d|(p-1) dans l'iso précédent.

par **barbu23** » 27 Jan 2010, 17:31

yos a écrit: donc les sous-groupes de Z/pZ* sont les préimages des dZ/(p-1)Z où d|(p-1) dans l'iso précédent.

Great ! et bien, c'est ce que je cherchais depuis le debut ! :zen:
Merci yos ! :happy3:

par **barbu23** » 28 Jan 2010, 14:19

Bonjour à tous : :happy3:
Je voudrais savoir quelles sont les éléments

- uplet de

qui s'écrivent comme ça :

avec

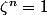
, tel que :

?
Merci d'avance ! :happy3:

par **Ben314** » 28 Jan 2010, 14:31

barbu23 a écrit:Bonjour à tous : :happy3:
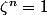
Je voudrais savoir quelles sont les éléments - uplet de qui s'écrivent comme ça : avec , tel que : ?
Merci d'avance ! :happy3:

Comme précédement, si tu n'écrit pas que

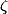
est une racine primitive, j'ais pas trop de mal à te donner un élément de réponse :
Pour

(qui vérifie bien

) je prend puis

et les autres nuls...

Est tu au moins allé jeté un coup d'oeil à ce qu'étaient les polynômes cyclotomiques ?
Si non, je te le conseille plus que vivement...

Un autre exemple (moins con) : n=4 ;

(racine primitive),

par **barbu23** » 28 Jan 2010, 14:35

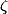
Ben314 a écrit:Comme précédement, si tu n'écrit pas que est une racine primitive, j'ais pas trop de mal à te donner un élément de réponse :
Pour (qui vérifie bien ) je prend puis et les autres nuls...

Est tu au moins allé jeté un coup d'oeil à ce qu'étaient les polynômes cyclotomiques ?
Si non, je te le conseille plus que vivement...

Oui, je connais les polynomes cyclotomique

:

, mais, moi, je cherche sur des exemple, un peu plus grand que ça, par exemple :

et sans que

soit premier, mais en general ! :happy3:

par **barbu23** » 28 Jan 2010, 14:37

Ah, d'accord, tu veux dire que les

- uplets sont ceux qui forment les coefficients de tous les polynomes cylotomiques de

! c'est bien alors ! merci ! :happy3:

par **Ben314** » 28 Jan 2010, 14:46

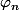
barbu23 a écrit:Ah, d'accord, tu veux dire que les - uplets sont ceux qui forment les coefficients de tous les multiples du polynome cylotomique ! c'est bien alors ! merci ! :happy3:

OUI, c'est ça

Racines unités

Qui est en ligne