DM Repères Seconde

par **Kléber** » 17 Jan 2015, 17:19

Bonjour/Bonsoir
Je suis actuellement en Seconde et nouveau sur ce forum ; j'ai un DM à rendre pour ce lundi et je bloque sur quelques questions mais j'ai des traces de recherche et si vous pouviez me dire si j'ai bien débuté serait géniale.Il me manque en effet quelques précisions et votre avis.
Donc le voici par Noelshack puisque c'est de la géométrie.
1er exercice :
http://www.noelshack.com/2015-03-1421510200-iphone-image-01-17-2015.jpg
Ma trace de recherche avec la figure tracée :
http://www.noelshack.com/2015-03-1421510433-iphone-image-01-17-2015.jpg
2ème exercice (algorithme)
http://www.noelshack.com/2015-03-1421510327-iphone-image-01-17-2015.jpg
Ma trace de recherche (dites c'est bon) : xA+xC=xB et yA+yC=yB alors "OABC" est un parallélogramme
http://www.noelshack.com/2015-03-1421511303-iphone-image-01-17-2015.jpg
Dernier exercice (Réflexion) :
http://www.noelshack.com/2015-03-1421511388-iphone-image-01-17-2015.jpg
Trace de recherche :
http://www.noelshack.com/2015-03-1421511493-iphone-image-01-17-2015.jpg
Excusez-moi pour la qualité des images.
Ce dont je ne comprends pas c'est comment calculer la longueur des segments puisque le repère n'est pas orthonormé.N'hésitez pas à donner votre avis sur la démarche,et sur mes résultats.
Cordialement.

par **mathelot** » 17 Jan 2015, 17:35

pour le (1),

A,B,D étant un repère orthonormé tu peux considérer AB=AD=1

on connait les tous angles (CAD=45°) et on peut faire
- de la trigo, du calcul de tangente, du Thalès et du Pythagore

(par ex APM est isocèle rectangle)

pour la perpendicularité on peut remplacer PQ par MN et appliquer
la réciproque de Pythagore à BMN

par **mathelot** » 17 Jan 2015, 17:45

Kléber a écrit:Bonjour/Bonsoir
Je suis actuellement en Seconde et nouveau sur ce forum ; j'ai un DM à rendre pour ce lundi et je bloque sur quelques questions mais j'ai des traces de recherche et si vous pouviez me dire si j'ai bien débuté serait géniale.Il me manque en effet quelques précisions et votre avis.
Donc le voici par Noelshack puisque c'est de la géométrie.
1er exercice :
http://www.noelshack.com/2015-03-1421510200-iphone-image-01-17-2015.jpg
Ma trace de recherche avec la figure tracée :
http://www.noelshack.com/2015-03-1421510433-iphone-image-01-17-2015.jpg
2ème exercice (algorithme)
http://www.noelshack.com/2015-03-1421510327-iphone-image-01-17-2015.jpg
Ma trace de recherche (dites c'est bon) : xA+xC=2xB et yA+yC=2yB alors "OABC" est un parallélogramme
il s'agit que les diagonales aient même milieu
http://www.noelshack.com/2015-03-1421511303-iphone-image-01-17-2015.jpg
Dernier exercice (Réflexion) :
http://www.noelshack.com/2015-03-1421511388-iphone-image-01-17-2015.jpg
Trace de recherche :
http://www.noelshack.com/2015-03-1421511493-iphone-image-01-17-2015.jpg
Excusez-moi pour la qualité des images.
Ce dont je ne comprends pas c'est comment calculer la longueur des segments puisque le repère n'est pas orthonormé.N'hésitez pas à donner votre avis sur la démarche,et sur mes résultats.
Cordialement.

...............

la vérification à faire est la suivante

ABCD # si et seulement si (xA+xC):2=(xB+xD):2
pareil pour les ordonnnées un parallélogramme étant un quadrilatère dont les diagonales ont même milieu

pour le dernier exo on peut tjrs dire que le côté du plus petit carré vaut 1
et faire des calculs Pythagore-like.

par **mathelot** » 17 Jan 2015, 17:56

Kléber a écrit:Ce dont je ne comprends pas c'est comment calculer la longueur des segments puisque le repère n'est pas orthonormé.

c'est toi qui choisis l'unité. si tu as envie d'écrire AB=1
ça signifie que le référent est la distance AB.

ensuite on fait les calculs sans jamais être en contradiction avec cette définition posée.

si tu poses comme unité de longueur Terrre-Lune=1, ça veut dire
que ton meilleur pote n'habite pas à 50 mètres de chez toi mais à

u.l (unité de longueur) de ton domicile.

PS la méthode analytique (=travailler avec des coordonnnées) n'est pa tjrs la meilleure des méthode. Thalès, le calcul d'aires donnent égaleement de bons résultats.

par **Kléber** » 17 Jan 2015, 19:27

Déjà merci pour vos réponses ! Ensuite j'ai bossé de mon côté et voici ce que j'ai obtenu,
Exercice sur l'algorithme :
http://www.noelshack.com/2015-03-1421518806-iphone-image-01-17-2015.jpg

Exercice sur les longueurs :
http://www.noelshack.com/2015-03-1421518937-iphone-image-01-17-2015.jpg
http://www.noelshack.com/2015-03-1421519346-iphone-image-01-17-2015.jpg
J'ai trouvé racine de 41 et racine de 52 en appliquant Pythagore,après avoir changé les longueurs en carreaux minuscules comme ceux d'en haut.

En revanche,je n'ai toujours pas terminé celui sur les droites perpendiculaires. L'unité ok,mais comment exprimer l'ordonnée de M en fonction de x ?

par **Kléber** » 18 Jan 2015, 01:00

Merci pour vos réponses ! J'ai réussi 2 des exercices. En revanche,pourriez-vous m'éclairer sur le 1er ? Je cale toujours sur la question :"Exprimer l'ordonnée de M en fonction de X" à vrai dire je ne comprends pas vraiment la question.Et comment placer les coordonnées des différents points sur le carré en étant sûr que ce sont les bonnes.
Et si vous avez des astuces ou méthodes pour la suite de l'exercice elles sont les bienvenues.Puisqu'il faut démontrer les droites perpendiculaire avec la réciproque de Pythagore je crois.
Voici l'énoncé : http://www.noelshack.com/2015-03-1421538911-iphone-image-01-18-2015.jpg
Et voici ma progression ou plutôt ma stagnation :
http://www.noelshack.com/2015-03-1421539216-iphone-image-01-18-2015.jpg
1) X appartient à [0;1]
2) Exprimer l'ordonnée de M en fonction de x ? M(x; je ne sais pas)
3) P(0 ;-2/3 ) Q(2/3;-1) N(0;-1/3)
Je ne suis pas du tout sûr pour les coordonnées que j'ai marqué,mais visiblement on doit bosser avec pour prouver que les droites sont perpendiculaires.
Merci d'avance !

par **mathelot** » 18 Jan 2015, 10:31

ABCD est un carré.

résultat des courses, A,B,C,D est un repère orthonormé
tu peux dire A(0,0) B (1,0) C(1,-1) et D(0,-1)
ou choisir un autre repère (et les points auront d'autres cordonnées).

(AC) est la bisssectrice de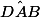

Sur une bissectrice, les points sont à égale distance des côtés de l'angle.

M a pour coordonnées (x,x) car il est sur la 1ère bissectrice du repère.

là deux options s'offrent à toi:

-la bovine, de calculer les coordonnées des points et d'écrire les équations
des droites en résolvant des systèmes y=mx+p d'inconnues m et p,

ou de dire directement les coorodnnées des points.

L'inconnu N se calcule en coordonnnées via

choisis bien ton repère r.o.n.

cordialement

par **mathelot** » 18 Jan 2015, 10:36

je vois où ça coince sur ton brouilllon.
Les coordonnées du point M sur la diagonale sont insuffisammment paramétrées.

i) choisis le repère o.n qui te chante
iii) par contre M doit avoir des coordonnées littérales (=avec des lettres)
pour dire qu'il peut être "mobile","indéfini","variable" sur cette diagonale.

par **Kléber** » 18 Jan 2015, 11:23

mathelot a écrit:ABCD est un carré.

résultat des courses, A,B,C,D est un repère orthonormé
tu peux dire A(0,0) B (1,0) C(1,-1) et D(0,-1)
ou choisir un autre repère (et les points auront d'autres cordonnées).

(AC) est la bisssectrice de

Sur une bissectrice, les points sont à égale distance des côtés de l'angle.

M a pour coordonnées (x,x) car il est sur la 1ère bissectrice du repère.

là deux options s'offrent à toi:

-la bovine, de calculer les coordonnées des points et d'écrire les équations
des droites en résolvant des systèmes y=mx+p d'inconnues m et p,

ou de dire directement les coorodnnées des points.

L'inconnu N se calcule en coordonnnées via

choisis bien ton repère r.o.n.

cordialement

Merci pour ta réponse ! Je vais explorer cette piste,par contre on n'a pas encore abordé les vecteurs en cours donc il doit y avoir une autre solution. Je vais essayer avec l'expression littérale que tu as proposé ainsi qu'avec les systèmes d'équations.

par **mathelot** » 18 Jan 2015, 11:41

queel repère o.n prends tu finalement ?
si tu prend l'orrigine en haut, ça fera des ssignes "-" pour les coordonnées.

si tu as compris que M(x,x) a ses coordonnnées égales car situé sur la diagonale,
alors c'est gagné.

n'hésite pas à utiliser Thalès (surtout), les angles dont les tangents sont constantes , et le calcul d'aire.

DM Repères Seconde

DM Repères Seconde

Qui est en ligne