EMV pour loi normal

[joanie58]

Bonjour,

soit des variables aléatoires identiquement distribuées suivant une loi normal

j'aimerais trouver l'estimateur du maximum de vraissemblance de .

Soit ma fonction de vraissemblance, j'ai considéré que et que

J'ai trouver que

Est-ce que c'est bien ce que je devais trouver? Et pour trouver mon EMV, je dois simplement trouver les maximum de cette fonction avec la dérivé première par rapport à et valider avec la dérivé seconde ?

[alegaxandra]

Exploite déjà ici la méthode du maximum de vraisemblance sous l'hypothèse de variables en distribution normale pour estimer les paramètres d'un modèle avec restrictions ou pas: http://tecfaetu.unige.ch/staf/staf-d/merino/staf18/cours/MV.html

[joanie58]

Bonjour,

j'ai une population de taille N ou l'on mesure deux variables: :le poids des individus et : leur tailles. On tire un échantillons de taille n.

soit x' l'estimateur pontuel du total de la variable X, y' l'estimateur pontuel du total de la variable Y

Est-ce qu'il est possible de montré que le coefficient de corrélation entre x' et y' est égale au coefficient de corrélation entre et

[alegaxandra]

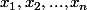
L'énoncé doit te dire que soit : des variables aléatoires identiquement distribuées suivant une loi normale: , le 1er paramètre étant la moyenne et le 2ème paramètre : l'écart-type. Pour l'estimateur de du maximum de vraisemblance, je trouve quant à moi, que la log-vraisemblance nous donne :
On sait calculer l'estimateur du Max de vraisemblance pour de la loi normale: [url=math.unice.fr/~diener/probas/Vraisembl.pdf]math.unice.fr/~diener/probas/Vraisembl.pdf[/url] avec la moyenne en estimateur de l'espérance. Une méthode alternative : le calcul de l'EMV de la loi pour les paramètres .

[alegaxandra]

@joanie58: peux-tu reposter la question effacée avant que quelqu'un n'y ait répondu dans les faits, sur la comparaison des loi suivies par les estimateurs ponctuels précis et sans biais par rapport à celles déductibles pour leurs variables associées ? Il est dommage de supprimer une réponse qui peut servir.

[joanie58]

désolé! je ne voulais pas poster la question ici... je voulais créer une nouvelle discussion et poser ma question dans une nouvelle discussion...je me suis rendu compte de mon erreur et j'ai effacé la question... je crois que dans les règlements du forum on ne dois poster qu'une interrogation par discussion ...