Intégrale curviligne d'une forme différentielle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 17 Nov 2014, 23:00
par Romanouch » 17 Nov 2014, 23:00
Bonjour,
Soit

un ouvert de

,
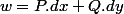
une forme différentielle continue sur

et
)
un chemin de [a;b] dans

. On appelle intégrale curviligne de w le long de

le réel:
}).x'(t)+Q(\lambda{(t)}).y'(t)).dt)
Je ne comprend pas pourquoi de
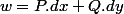
, on passe à
})=P(\lambda{(t)}).x'(t)+Q(\lambda{(t)}).y'(t))
en particulier, pourquoi
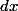
devient
)
et
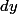
devient
)
.
Merci d'avance.
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 18 Nov 2014, 00:21
par mrif » 18 Nov 2014, 00:21
Romanouch a écrit:Bonjour,
Soit

un ouvert de

,
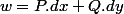
une forme différentielle continue sur

et
)
un chemin de [a;b] dans

. On appelle intégrale curviligne de w le long de

le réel:
}).x'(t)+Q(\lambda{(t)}).y'(t)).dt)
Je ne comprend pas pourquoi de
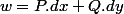
, on passe à
})=P(\lambda{(t)}).x'(t)+Q(\lambda{(t)}).y'(t))
en particulier, pourquoi
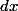
devient
)
et
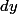
devient
)
.
Merci d'avance.
Il manque un
dt dans ta dernière égalité:
})=P(\lambda{(t)}).x'(t)+Q(\lambda{(t)}).y'(t))
Le chemin

est une application de
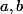
dans

définie par:
 = (x(t),y(t)))
.
On a donc par définition:
dt)
et
dt)
et ta dernière formule devient:
})=P((\lambda{(t)}).x'(t)+Q(\lambda{(t)}).y'(t))dt)
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 18 Nov 2014, 09:21
par Romanouch » 18 Nov 2014, 09:21
mrif a écrit:Il manque un
dt dans ta dernière égalité:
})=P(\lambda{(t)}).x'(t)+Q(\lambda{(t)}).y'(t))
Le chemin

est une application de
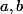
dans

définie par:
 = (x(t),y(t)))
.
On a donc par définition:
dt)
et
dt)
et ta dernière formule devient:
})=P((\lambda{(t)}).x'(t)+Q(\lambda{(t)}).y'(t))dt)
Bonjour,
Oui, il manque dt.
Soit x une fonction d'une variable t:
<br />\end{array}<br />\right.)
Alors, par définition de la différentielle:
.dt)
C'est bien ça?
-
mrif
- Membre Rationnel
- Messages: 527
- Enregistré le: 18 Mar 2013, 21:26
-
 par mrif » 18 Nov 2014, 10:35
par mrif » 18 Nov 2014, 10:35
Romanouch a écrit:Bonjour,
Oui, il manque dt.
Soit x une fonction d'une variable t:
<br />\end{array}<br />\right.)
Alors, par définition de la différentielle:
.dt)
C'est bien ça?
Oui, avec l'hypothèse que x est une fonction dérivable définie sur un ouvert de R.
-
Romanouch
- Membre Relatif
- Messages: 138
- Enregistré le: 19 Jan 2013, 20:34
-
 par Romanouch » 18 Nov 2014, 11:20
par Romanouch » 18 Nov 2014, 11:20
mrif a écrit:Oui, avec l'hypothèse que x est une fonction dérivable définie sur un ouvert de R.
Ok, merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
un ouvert de
,
une forme différentielle continue sur
et
un chemin de [a;b] dans
. On appelle intégrale curviligne de w le long de
le réel:
, on passe à
devient
et
devient
.