Résolution d'une équation de puissance

par **MacErmite** » 08 Nov 2014, 05:21

Bonjour ,

Je ne parviens pas à trouver une méthode permettant de résoudre l'équation ci-dessous. Je cherche l'expression de x et une seconde expression afin d'isoler b

Pouvez-vous m'éclairer ?

Merci.

par **mathelot** » 08 Nov 2014, 06:36

en passant au log:

ou x=-rb sqrt(|2/ln(a)|)

par **chan79** » 08 Nov 2014, 08:26

mathelot a écrit:

salut

Il est nécessaire que 0<a<1 pour que l'égalité ci-dessus soit possible.
Si x est solution, -x l'est aussi

par **MacErmite** » 08 Nov 2014, 15:39

mathelot a écrit:

en passant au log:

ou

Merci pour votre aide.

par **zygomatique** » 08 Nov 2014, 17:32

MacErmite a écrit:Bonjour ,

Je ne parviens pas à trouver une méthode permettant de résoudre l'équation ci-dessous. Je cherche l'expression de x et une seconde expression afin d'isoler b

Pouvez-vous m'éclairer ?

Merci.

salut

et on reconnaît

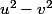
lorsque 0 < a < 1

il y a donc deux solutions opposées ...

:zen:

Résolution d'une équation de puissance

Résolution d'une équation de puissance

Qui est en ligne