Equations équivalentes

[TooLate]

Bonjour,
Étant en première S, j'aurais besoin d'un petit coup de pouce sur un exercice de maths...
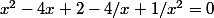
Il s'agit de démontrer que les équations et sont équivalentes. Seulement je ne vois pas trop comment faire :triste:
Si quelqu'un pouvait m'aider ce serait génial, merci beaucoup ! :zen:
:mur:

[ophel62bp]

Bonjour,
un petit indice : essaye de te "débarrasser" des quotients, en maths on n'aime pas trop les fractions... Pour cela, multiplie la deuxième équation par x²... :lol3:
ophel62bp

[TooLate]

Pour cela, multiplie la deuxième équation par x²
ophel62bp

Ah c'est autorisé ça ? Je savais pas...
... C'est génial :doh:
Merci beaucoup !! :euh:

[ophel62bp]

Pourquoi ce ne serait pas autorisé, x² est un nombre comme les autres... :we:
c'est comme si tu multipliais tout par 9, 25 ou n'importe quel nombre :lol3:
ophel62bp

[TooLate]

Je vois :we: J'y avais pas du tout pensé :marteau:
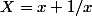
Par contre un peu plus loin dans l'exercice je dois montrer que l'équation (toujours la même : ) est équivalente au système [FONT=Arial Black]&[/FONT]
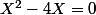
Les X en majuscules dans mon système y sont en majuscules dans l'exercice, ça a son importance ou ce serait plutôt une faute de frappe ? C'est toujours la même variable x ?
Merci encore :lol3:

[ophel62bp]

Oui, ça a une importance mais comme ça je peux pas te dire à quoi ils servent...
Peux-tu mettre l'énoncé complet de ton exercice stp ?
ophel62bp

[TooLate]

L'énoncé complet :
Soit (E) l'équation .
a) Vérifier que 0 n'est pas solution de (E).
b) Démontrer que si est solution de (E) alors est solution de (E).
c) Démontrer que l'équation (E) est équivalente à l'équation
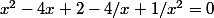
d) Développer
e) Démontrer que (E) est équivalente à
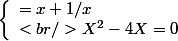
f) En déduire les solutions de (E) et vérifier qu'elles sont inverses l'une de l'autre.

J'ai répondu au a) et au b) seul, au c) avec ton aide ophel62bp, au d) seul et j'en suis arrivé au e) sans comprendre ces majuscules..

Merci beaucoup encore une fois ! :zen:

[ophel62bp]

J'ai compris... :marteau:
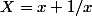
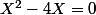
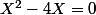
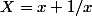
En fait dans ton exercice à la question e), on pose et on essaye de démontrer que ton équation est égale à . Pour vérifier cette équivalence, on doit remplacer X dans l'expression par la valeur qu'on lui a associé, à savoir . On a donc : et quand on simplifie on retrouve l'équation de la question c)... donc c'est bien équivalent :lol3:

[TooLate]

Ah très bien merci beaucoup ! Je pense que je peux continuer mon DM tout seul maintenant :id:
Personnellement je pense qu'il aurait quand même été plus clair de poser une autre lettre que x là où il y a des X majuscules... Pourquoi pas y ? Ou j ? On a un alphabet de 26 lettres autant les utiliser :ptdr:
Enfin peut-être que X a une signification spéciale... Enfin peu importe merci !
Au revoir ! :+++: