Tangente
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mathelot
 par mathelot » 25 Oct 2014, 13:43
par mathelot » 25 Oct 2014, 13:43
bibiceboss a écrit:Donc l'équation de ma tangente est fausse ?
Et la bonne equation est y=-x+3 c'est sa ?
Franchement je suis pommé..
l'équation de la tangente est
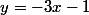
(cf. supra)
bibiceboss a écrit:y=-3x-1 est l'équation de la tangente en x=-1
C'est sa ?
oui, c'est moi qui déc******ais.
tu veux qu'on regarde la question (2) ?
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 13:49
par bibiceboss » 25 Oct 2014, 13:49
mathelot a écrit:l'équation de la tangente est
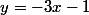
(cf. supra)
oui, c'est moi qui déc******ais.
tu veux qu'on regarde la question (2) ?
Ah d'accord merci beaucoup, par contre je coince sur cette question la aussi:
la courbe de la fonction g admet t-elle une tangente parallèle ?
-
mathelot
 par mathelot » 25 Oct 2014, 13:55
par mathelot » 25 Oct 2014, 13:55
Propriétédeux droites d'équations respectives

et
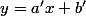
sont parallèles ssi
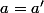
il te faut résoudre l'équation aux abscisses
=-3)
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 14:10
par bibiceboss » 25 Oct 2014, 14:10
mathelot a écrit:Propriétédeux droites d'équations respectives

et
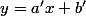
sont parallèles ssi
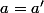
il te faut résoudre l'équation aux abscisses
=-3)
g(x)= 1/x
g'(x)=-1/x^2
g'(-3)= ?
C'est sa qu'il faut que je fasse ?
-
mathelot
 par mathelot » 25 Oct 2014, 14:14
par mathelot » 25 Oct 2014, 14:14
qu'est ce qu'est g'(x) du point de vue de la géométrie ?
qu'est ce qu'est le coefficient
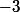
, dans l'équation
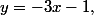
du point de vue de la
géométrie ?
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 14:19
par bibiceboss » 25 Oct 2014, 14:19
mathelot a écrit:qu'est ce qu'est g'(x) du point de vue de la géométrie ?
qu'est ce qu'est le coefficient
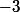
, dans l'équation
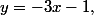
du point de vue de la
géométrie ?
g'(x) est la dérivée
-3 est le coefficient directeur de la droite
-
mathelot
 par mathelot » 25 Oct 2014, 14:32
par mathelot » 25 Oct 2014, 14:32
bibiceboss a écrit:g'(x) est la dérivée de g et le coefficient
de la tangente à C(g) au point de la courbe de g d'abscisse x
-3 est le coefficient directeur de la droite tangente à la courbe de f au point d'abscisse -1
..........................
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 14:38
par bibiceboss » 25 Oct 2014, 14:38
mathelot a écrit:..........................
Oui voilaa
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 14:58
par bibiceboss » 25 Oct 2014, 14:58
Mais donc je sais toujours pas comment avancer :/
-
mathelot
 par mathelot » 25 Oct 2014, 15:02
par mathelot » 25 Oct 2014, 15:02
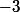
est le coefficient directeur de T
)
le coefficient directeur de la tangente à C(g) en L(x;g(x))
On demande pour quelles valeurs de

les deux tangentes sont parallèles.
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 15:05
par bibiceboss » 25 Oct 2014, 15:05
mathelot a écrit: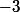
est le coefficient directeur de T
)
le coefficient directeur de la tangente à C(g) en L(x;g(x))
On demande pour quelles valeurs de

les deux tangentes sont parallèles.
Il faut que la parallele ait le meme coeff directeur c-a-d -3
-
mathelot
 par mathelot » 25 Oct 2014, 15:34
par mathelot » 25 Oct 2014, 15:34
oui:::::::::::::::
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 15:35
par bibiceboss » 25 Oct 2014, 15:35
mathelot a écrit:oui:::::::::::::::
Mais je comprends pas comment écrire sa
-
mathelot
 par mathelot » 25 Oct 2014, 15:45
par mathelot » 25 Oct 2014, 15:45
=\frac{-1}{x^2}=-3)
sauf erreur
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 15:52
par bibiceboss » 25 Oct 2014, 15:52
mathelot a écrit:=\frac{-1}{x^2}=-3)
sauf erreur
Il me reste juste a faire l'équation après c'est sa ?
-
mathelot
 par mathelot » 25 Oct 2014, 15:55
par mathelot » 25 Oct 2014, 15:55
oui:::::::::::::::
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 16:17
par bibiceboss » 25 Oct 2014, 16:17
mathelot a écrit:oui:::::::::::::::
x= 3 ?
C'est sa ?
-
mathelot
 par mathelot » 25 Oct 2014, 16:39
par mathelot » 25 Oct 2014, 16:39
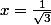
ou

?
-
bibiceboss
- Membre Naturel
- Messages: 29
- Enregistré le: 23 Oct 2014, 11:42
-
 par bibiceboss » 25 Oct 2014, 16:40
par bibiceboss » 25 Oct 2014, 16:40
mathelot a écrit: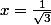
ou

?
Comment etes vous arriver a cela ?
-
mathelot
 par mathelot » 25 Oct 2014, 16:51
par mathelot » 25 Oct 2014, 16:51

passe à l'inverse..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
