Equation d'une sphère
14 messages
- Page 1 sur 1
Equation d'une sphère
Bonjour je recherche la solution de ce problème :
Cherchez l'équation de la sphère passant par les points (0;0;0), (2;2;4) et (4;4;2) et de rayon = 3*racine de 3
Merci de votre réponse :ptdr:
Cherchez l'équation de la sphère passant par les points (0;0;0), (2;2;4) et (4;4;2) et de rayon = 3*racine de 3
Merci de votre réponse :ptdr:
Bonjour,
La géométrie n'étant pas mon grand domaine de prédilection, je pense être néanmoins en mesure de t'aider ! ^^
L'équation d'une sphère est : (x-a)²+(y-b)²+(z-c)²=r² avec M(a,b,c) le centre de la sphère et r le rayon.
Il suffirait donc que tu remplaces chaque x,y,z par les coordonnées d'un point qui te sont donnés, ce qui te ramènera à un système de 3 équations et 3 inconnues ( a,b,c) que tu vas déterminer en résolvant le système ! :)
La géométrie n'étant pas mon grand domaine de prédilection, je pense être néanmoins en mesure de t'aider ! ^^
L'équation d'une sphère est : (x-a)²+(y-b)²+(z-c)²=r² avec M(a,b,c) le centre de la sphère et r le rayon.
Il suffirait donc que tu remplaces chaque x,y,z par les coordonnées d'un point qui te sont donnés, ce qui te ramènera à un système de 3 équations et 3 inconnues ( a,b,c) que tu vas déterminer en résolvant le système ! :)
Effectivement, ton système est assez déroutant; tu dois développer les 2 équations qui ne le sont pas; tu obtiens (1) (2) et (3); en faisant (1)-(2), (1)-(3) et (2)-(3), tu élimine les carrés et tu obtient un système d'inconnues a, b et c; mais ce système n'a pas de solution unique.
Pour te guider, tu dois trouver facilement c=1, puis b en fonction de a ce qui te permet de remplacer dans a²+b²+c²=27 et de trouver les 2 valeurs de a. :we:
Pour te guider, tu dois trouver facilement c=1, puis b en fonction de a ce qui te permet de remplacer dans a²+b²+c²=27 et de trouver les 2 valeurs de a. :we:
Salut,
Perso, si on note O:(0,0,0) ; A:(2,2,4) et B:(4,4,2), j'aurais commencé par chercher les équation des plan médiateurs de [OA] et [OB] (plan médiateur = plan passant par le milieu du segment et perpendiculaire au segment = ensemble des points équidistants des extrémités du segment)
Celui du segment [OA] a pour vecteur normal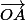 et passe par le milieu (1,1,2) donc a pour équation
et passe par le milieu (1,1,2) donc a pour équation 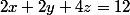 .
.
De même celui de [OB] a pour équation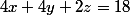 .
.
L'intersection de ces deux plan est la droite constitué des points équidistants de O,A et B donc c'est l'ensemble des centres de toutes les sphères passant par les trois points.
+z=9}\right.\ \Leftrightarrow\ <br />\left\{\matrix{y=4-x\cr z=1\ \ \ \ \ \ }\right.)
Il n'y a plus qu'à chercher parmi les points de coordonnées) celui qui est situé à une distance de
celui qui est situé à une distance de 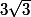 de
de  :
:
^2+1^2}=3\sqrt{3}\ \Leftrightarrow\ \cdots)
On pourrait aussi chercher l'intersection de cette droite avec le plan (OAB) pour avoir le centre du cercle passant par O,A et B puis calculer le rayon de ce cercle et utiliser Pyrhagore pour savoir à quelle distance on doit se situer (sur la droite) du centre du cercle pour être à une distance de
du cercle passant par O,A et B puis calculer le rayon de ce cercle et utiliser Pyrhagore pour savoir à quelle distance on doit se situer (sur la droite) du centre du cercle pour être à une distance de 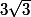 des 3 points (il y a évidement deux solutions de part et d'autre du plan en question).
des 3 points (il y a évidement deux solutions de part et d'autre du plan en question).
On peut aussi remarquer que, parmi les points) , le centre du cercle est celui qui minimise
, le centre du cercle est celui qui minimise ^2+1^2) ...
...
Perso, si on note O:(0,0,0) ; A:(2,2,4) et B:(4,4,2), j'aurais commencé par chercher les équation des plan médiateurs de [OA] et [OB] (plan médiateur = plan passant par le milieu du segment et perpendiculaire au segment = ensemble des points équidistants des extrémités du segment)
Celui du segment [OA] a pour vecteur normal
De même celui de [OB] a pour équation
L'intersection de ces deux plan est la droite constitué des points équidistants de O,A et B donc c'est l'ensemble des centres de toutes les sphères passant par les trois points.
Il n'y a plus qu'à chercher parmi les points de coordonnées
On pourrait aussi chercher l'intersection de cette droite avec le plan (OAB) pour avoir le centre
On peut aussi remarquer que, parmi les points
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'avais fait comme paquito et Teamynil
a²+b²+c²=27 ( 1)
(2-a)²+(2-b)²+(4-c)²=27 (2)
(4-a)²+(4-b)²+(2-c)²=27 (3)
(1) et (2) donnent 2a+2b+4c=12
(1) et (3) donnent 2a+2b+c=9
donc c=1
a+b=4
a²+b²=26
En élevant au carré (a+b), 16=26+2ab donc ab=-5
a et b sont solutions de X²-4X-5=0
(a,b,c)=(5,-1,1) ou (-1,5,1)
a²+b²+c²=27 ( 1)
(2-a)²+(2-b)²+(4-c)²=27 (2)
(4-a)²+(4-b)²+(2-c)²=27 (3)
(1) et (2) donnent 2a+2b+4c=12
(1) et (3) donnent 2a+2b+c=9
donc c=1
a+b=4
a²+b²=26
En élevant au carré (a+b), 16=26+2ab donc ab=-5
a et b sont solutions de X²-4X-5=0
(a,b,c)=(5,-1,1) ou (-1,5,1)
Ben314 a écrit:Salut,
Perso, si on note O:(0,0,0) ; A:(2,2,4) et B:(4,4,2), j'aurais commencé par chercher les équation des plan médiateurs de [OA] et [OB] (plan médiateur = plan passant par le milieu du segment et perpendiculaire au segment = ensemble des points équidistants des extrémités du segment)
Celui du segment [OA] a pour vecteur normalet passe par le milieu (1,1,2) donc a pour équation
.
De même celui de [OB] a pour équation.
L'intersection de ces deux plan est la droite constitué des points équidistants de O,A et B donc c'est l'ensemble des centres de toutes les sphères passant par les trois points.
Il n'y a plus qu'à chercher parmi les points de coordonnéescelui qui est situé à une distance de
de
:
On pourrait aussi chercher l'intersection de cette droite avec le plan (OAB) pour avoir le centredu cercle passant par O,A et B puis calculer le rayon de ce cercle et utiliser Pyrhagore pour savoir à quelle distance on doit se situer (sur la droite) du centre du cercle pour être à une distance de
des 3 points (il y a évidement deux solutions de part et d'autre du plan en question).
On peut aussi remarquer que, parmi les points, le centre du cercle est celui qui minimise
...
Pourquoi faire simple quand on peut faire compliqué! Je ne vois pas un élève de TS adopter ton raisonnement, même s'il est joli! Il faut rester abordable!
chan79 a écrit:J'avais fait comme paquito et Teamynil
a²+b²+c²=27 ( 1)
(2-a)²+(2-b)²+(4-c)²=27 (2)
(4-a)²+(4-b)²+(2-c)²=27 (3)
(1) et (2) donnent 2a+2b+4c=12
(1) et (3) donnent 2a+2b+c=9
donc c=1
a+b=4
a²+b²=26
En élevant au carré (a+b), 16=26+2ab donc ab=-5
a et b sont solutions de X²-4X-5=0
(a,b,c)=(5,-1,1) ou (-1,5,1)
Ca, c'est abordable pour un élève de TS!
paquito a écrit:Pourquoi faire simple quand on peut faire compliqué! Je ne vois pas un élève de TS adopter ton raisonnement, même s'il est joli! Il faut rester abordable!
C'est vrai : écrire un système non linéaire de 3 équations à 3 inconnues est bien plus "abordable" que d'utiliser ce qu'il y a dans le programme de géométrie de terminale, à savoir la notion d'équation de plan et de vecteur normal...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
paquito a écrit:Ca, c'est abordable pour un élève de TS!
Et je rajouterais que le fait de faire l'équation (1)-(2), c'est ce qu'ils ont fait en cours lorsqu'ils ont étudié la notion de plan médiateur...
Résumé : pourquoi diable démontrer des trucs en cours vu qu'on s'en sert pas...
P.S. ça m'intéresserait fortement de savoir quelle est la solution proposé par le prof. de chauvinou pour cet exercice
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
[quote="chan79"]J'avais fait comme paquito et Teamynil
a²+b²+c²=27 ( 1)
(2-a)²+(2-b)²+(4-c)²=27 (2)
(4-a)²+(4-b)²+(2-c)²=27 (3)
(1) et (2) donnent 2a+2b+4c=12
(1) et (3) donnent 2a+2b+c=9
donc c=1
a+b=4
Remarque ( avec O(0;0;0) A(2;02;4) et B(4;4;2))
2a+2b+4c=12 est l'équation du plan médiateur de [OA]
2a+2b+c=9 est l'équation du plan médiateur de [OB]
Le système formé par ces deux équations définissent la droite d'intersection de ces deux plans(elle est incluse dans le plan c=1)
Les deux centres cherchés sont les deux points d'intersection de cette droite avec par exemple la sphère d'équation x²+y²+z²=27
a²+b²+c²=27 ( 1)
(2-a)²+(2-b)²+(4-c)²=27 (2)
(4-a)²+(4-b)²+(2-c)²=27 (3)
(1) et (2) donnent 2a+2b+4c=12
(1) et (3) donnent 2a+2b+c=9
donc c=1
a+b=4
Remarque ( avec O(0;0;0) A(2;02;4) et B(4;4;2))
2a+2b+4c=12 est l'équation du plan médiateur de [OA]
2a+2b+c=9 est l'équation du plan médiateur de [OB]
Le système formé par ces deux équations définissent la droite d'intersection de ces deux plans(elle est incluse dans le plan c=1)
Les deux centres cherchés sont les deux points d'intersection de cette droite avec par exemple la sphère d'équation x²+y²+z²=27
Ben314 a écrit:C'est vrai : écrire un système non linéaire de 3 équations à 3 inconnues est bien plus "abordable" que d'utiliser ce qu'il y a dans le programme de géométrie de terminale, à savoir la notion d'équation de plan et de vecteur normal...
Salut, ben,
En fait si on avait 3 points non alignés dans le plan je suis certain que très peu d'élèves auraient utilisé l'intersection de deux médiatrices. Déjà quand on demande le lieu des points M qui vérifient MA=MB, c'est le grand silence, et en complexes, c'est le blocage assuré.
Le problème c'est que l'on élude toute ce qui est géométrie pure au profit de l'analytique qui ne peut pas donner une bonne vision dans l'espace.
Sinon ta démarche est très intéressante et pourrait faire l'objet d'un petit devoir à la maison dans une bonne TS.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
