Transformation de fourier
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 12:31
par pseudodupseudo » 19 Mai 2014, 12:31
Bonjour,
pourriez vous m'indiquez svp comment résoudre cet exercice.
je dois calculer la transformation de h :
=e^{i\alpha x}f(x))
Merci de votre aide.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Mai 2014, 15:44
par adrien69 » 19 Mai 2014, 15:44
Salut.
Est-ce que tu as au moins essayé ? Parce que bon, là c'est un peu juste un calcul...
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 19 Mai 2014, 15:50
par Cliffe » 19 Mai 2014, 15:50
[CENTER]
 = \int_{- \infty}^{\infty} h(x)e^{-itx}dx)
[/CENTER]
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 15:58
par pseudodupseudo » 19 Mai 2014, 15:58
Bonjour à vous deux,
j'ai bien entendu essayé, mais il y a quelque chose que je ne comprend pas. Une fois que j'ai mon h(x) dans la formule, je met les exponentiels ensembles ce qui me donne
ix})
, mais je fais quoi du f(x) restant dans mon intégrale ?
Merci.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 19 Mai 2014, 16:01
par Cliffe » 19 Mai 2014, 16:01
tu le remplace par son expression
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Mai 2014, 16:09
par adrien69 » 19 Mai 2014, 16:09
Cliffe a écrit:tu le remplace par son expression
Euh non... T'y touches surtout pas, façon tu l'as pas l'expression.
Faut juste que tu fasses un changement de variables.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Mai 2014, 16:11
par Sylviel » 19 Mai 2014, 16:11
petit hint : tu as peut-être le droit de donner le résultat en fonction de la transformée de Fourier de f :zen:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 16:13
par pseudodupseudo » 19 Mai 2014, 16:13
adrien69 a écrit:Euh non... T'y touches surtout pas, façon tu l'as pas l'expression.
Faut juste que tu fasses un changement de variables.
j'ai donc
 = \int_{- \infty}^{\infty} f(x)e^{(\alpha -t)ix}dx)
Je dois faire un changement de variable de quoi svp ?
car je ne connais pas f(x)
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 16:15
par pseudodupseudo » 19 Mai 2014, 16:15
Sylviel a écrit:petit hint : tu as peut-être le droit de donner le résultat en fonction de la transformée de Fourier de f :zen:
je ne comprend plus là, je commence à décrocher :ptdr:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Mai 2014, 16:23
par Sylviel » 19 Mai 2014, 16:23
Que vaut la transformmée de fourier de f en un point b ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 16:27
par pseudodupseudo » 19 Mai 2014, 16:27
Sylviel a écrit:Que vaut la transformmée de fourier de f en un point b ?
Je ne pense pas comprendre la question, mais je dirais que cela vaut:
 = \int_{- \infty}^{b} f(x)e^{-itx}dx)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Mai 2014, 16:32
par Sylviel » 19 Mai 2014, 16:32
Sauf que là tu as écrit t au lieu de b, et un h au lieu de f. Et tu ne vois aucun lien avec la formule du dessus ?
edit : ah non, tu as changé les bornes de l'intégrale :dodo:
Moi je te demande juste la valeur de la tranformée de f au point b. Donc tu prends tout bêtement ta formule (celle que tu nous as donné avec h) et tu remplaces t par b, pas plus :id:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 16:38
par pseudodupseudo » 19 Mai 2014, 16:38
Sylviel a écrit:Sauf que là tu as écrit t au lieu de b, et un h au lieu de f. Et tu ne vois aucun lien avec la formule du dessus ?
ah désolé je n'ai pas fait attention.
Non, je ne vois pas quel est le lien entre
 = \int_{- \infty}^{\infty} f(x)e^{(\alpha -t)ix}dx)
et la formule du dessus.
Je pense ne pas avoir la bonne approche de la transformé de Fourier, car vous me parler d'une transformé de fourier en un point, mais dans ce que je cherche initialement, ca n'évoque nulle part un point.
Pourriez vous m'expliquer cela svp.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Mai 2014, 16:41
par adrien69 » 19 Mai 2014, 16:41
Tu n'évaluerais pas
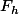
au point t quand tu écris
)
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 16:44
par pseudodupseudo » 19 Mai 2014, 16:44
adrien69 a écrit:Tu n'évaluerais pas
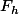
au point t quand tu écris
)
Vous voulez dire quoi par "évaluer "?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Mai 2014, 16:51
par Sylviel » 19 Mai 2014, 16:51
Ben tu as une fonction u : R -> R. Evaluer u au point b c'est calculer u(b), rien d'autres !
La transformée de Fourier de f c'est bien une fonction de R dans R, et habituellement tu l'évalues en t dans ton cours visiblement.
Ces deux intégrales ne se ressemblent pas d'après toi ?
e^{(\alpha -t)ix}dx)
e^{-b ix}dx)
Le première c'est la tranformée de h évaluée au point t, la seconde la transformée de f évaluée au point b.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
pseudodupseudo
- Membre Naturel
- Messages: 39
- Enregistré le: 10 Avr 2012, 09:53
-
 par pseudodupseudo » 19 Mai 2014, 17:01
par pseudodupseudo » 19 Mai 2014, 17:01
Sylviel a écrit:Ben tu as une fonction u : R -> R. Evaluer u au point b c'est calculer u(b), rien d'autres !
La transformée de Fourier de f c'est bien une fonction de R dans R, et habituellement tu l'évalues en t dans ton cours visiblement.
Ces deux intégrales ne se ressemblent pas d'après toi ?
e^{(\alpha -t)ix}dx)
e^{-b ix}dx)
Le première c'est la tranformée de h évaluée au point t, la seconde la transformée de f évaluée au point b.
j'aurais appris un nouveau terme "évaluer" :lol3:
Je viens de comprendre, où vous vouliez en venir avec le changement de variable et la transformé de fourier en un point.
J'ai donc
 = \int_{- \infty}^{\infty} f(x)e^{\alpha ix}e^{-itx}dx = = \int_{- \infty}^{\infty} f(x)e^{{\alpha-t}ix}dx)
on effectue un changement de variable avec

j'obtient donc:
 = \int_{- \infty}^{\infty} f(x)e^{-bix}dx)
est ce que c'est celà ?
(il s'agissait d'application de formule de cours en fait)
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Mai 2014, 17:07
par adrien69 » 19 Mai 2014, 17:07
Faux.
Dans changement de VARIABLE, il y a le mot VARIABLE.
Toi tu changes un truc qui ne varie pas (t et alpha sont fixés !)
Donc il faut que tu trouves un y=g(x) qui t'arrange (pour une certaine fonction g).
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 19 Mai 2014, 17:08
par Sylviel » 19 Mai 2014, 17:08
Ouaip, c'est la démonstration d'une formule que tu as sans doute vu en cours. En réalité tu dois arriver à faire le calcul de tête avec un peu d'habitude :zen:
Dans le même genre tu peux t'entrainer à calculer la transformée de Fourier de
x -> f(2x)
x -> f(-x)
x -> f(ax +b)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 19 Mai 2014, 17:10
par adrien69 » 19 Mai 2014, 17:10
Si quelqu'un a vu ce que j'ai écrit juste avant, je me suis laissé emporter par mon propre exo, navré ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités