Fonctions dérivées (Terminale S)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Snailfire
- Messages: 6
- Enregistré le: 15 Avr 2014, 09:49
-
 par Snailfire » 15 Avr 2014, 10:47
par Snailfire » 15 Avr 2014, 10:47
[FONT=Comic Sans MS]
Bonjour,
Je suis actuellement en BTS par correspondance, et j'essaye de me remettre à niveau en Maths.
En effet cela fait plusieurs années que je n'ai pas repris mes études et j'ai quelques lacunes.
Dans l'ensemble je comprends, mais c'est dans les calculs intermédiaire que je n'y arrive pas.
Je perds énormément de temps à faire des brouillons et des recherches sur chaque exercices...
Je vous présente mon exercice:[/FONT]
Pour chacune des fonctions suivantes, déterminer son domaine de définition, calculer la fonction dérivée, et déterminer le domaine de définition de la fonction dérivée.
1.
=x(sqrt{x}+1)^3)
2.
=\frac{x^2+1}{2-x})
3.
=sqrt{\frac{x^2-x+2}{x(x+1)}})
Je commence par le n°1:
Le domaine de définition de
=x(sqrt{x}+1)^3)
est

.

donc

et
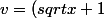^3 ; v'=3(\frac{1}{2sqrt{x}})^2)
C'est ici que je bloque, je ne suis pas sûr de la dérivée de v. :triste:
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 15 Avr 2014, 11:11
par paquito » 15 Avr 2014, 11:11
La dérivée de U^3 est 3u'u²; il y a un petit mélange; toi tu appliques (u^3)'=3u'².
((Vx+1)^3)'=3(1/2Vx)(Vx+1)².
-
Snailfire
- Messages: 6
- Enregistré le: 15 Avr 2014, 09:49
-
 par Snailfire » 15 Avr 2014, 11:28
par Snailfire » 15 Avr 2014, 11:28
Merci si je comprend bien on a
(sqrt{x}+1)^2)
et c'est = à
^2}{2sqrt{x}}))
= à
)
= à

et donc [TEX]\frac{3}{sqrt{x}} ?
-
Snailfire
- Messages: 6
- Enregistré le: 15 Avr 2014, 09:49
-
 par Snailfire » 15 Avr 2014, 11:30
par Snailfire » 15 Avr 2014, 11:30
ZUT !
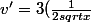(sqrt{x}+1)^2)
et à la fin:

-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 15 Avr 2014, 12:23
par paquito » 15 Avr 2014, 12:23
Snailfire a écrit:ZUT !
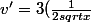(sqrt{x}+1)^2)
et à la fin:

3/Vx!!!!! Je ne vois pas comment tu peux trouver ça f'(x)=(Vx+1)^3+3x(1/2Vx)(Vx+1)²=(Vx+1)²((Vx+1)+3x/2Vx)=(Vx+1)(2x+2Vx+3x)/2Vx du signe de 5x+2Vx>0 pour x>0
-
Snailfire
- Messages: 6
- Enregistré le: 15 Avr 2014, 09:49
-
 par Snailfire » 17 Avr 2014, 11:07
par Snailfire » 17 Avr 2014, 11:07
paquito a écrit:3/Vx!!!!! Je ne vois pas comment tu peux trouver ça f'(x)=(Vx+1)^3+3x(1/2Vx)(Vx+1)²=(Vx+1)²((Vx+1)+3x/2Vx)=(Vx+1)(2x+2Vx+3x)/2Vx du signe de 5x+2Vx>0 pour x>0
Excusez mon absence...
Donc OK,
u=x ; u'=1
v=(Vx+1)^3 ; v'=3(1/2Vx)(Vx+1)^2
f(x)=uv ; f'(x)=u'v+uv'
f'(x)=(Vx+1)^3+3x(1/2Vx)(Vx+1)^2
f'(x)=(Vx+1)^2((Vx+1)+3x/2Vx) Je comprend jusque là.
f'(x)=(Vx+1)((2x+2Vx+3x)/2Vx) Pourquoi la puissance 2 du premier terme n'est plus là?
après j'ai fait:
f'(x)=(Vx+1)(2Vx+5x/2Vx)
f'(x)=5x(Vx+1) Comment calculer 5x(Vx) ? (je bug)
Merci
-
Snailfire
- Messages: 6
- Enregistré le: 15 Avr 2014, 09:49
-
 par Snailfire » 17 Avr 2014, 12:30
par Snailfire » 17 Avr 2014, 12:30
Ça doit faire 5xVx+1 en fait tout simplement...?
-
Black Jack
 par Black Jack » 17 Avr 2014, 13:57
par Black Jack » 17 Avr 2014, 13:57
Pas d'accord déjà avec le domaine pour la 1
f(x) = x(Vx + 1)³
Df = R+ (et pas R*+)
f'(x) = (Vx + 1)³ + 3x.(Vx + 1)²/(2Vx)
f'(x) = (Vx + 1)³ + (3/2).Vx.(Vx + 1)²
f'(x) = (Vx + 1)² * [(Vx + 1) + (3/2).Vx]
f'(x) = (Vx + 1)² * ((5/2).Vx + 1)
f'(x) = (1/2).(Vx + 1)² * (5Vx + 2)
Df' = R+
:zen:
-
Snailfire
- Messages: 6
- Enregistré le: 15 Avr 2014, 09:49
-
 par Snailfire » 21 Avr 2014, 12:46
par Snailfire » 21 Avr 2014, 12:46
Black Jack a écrit:Pas d'accord déjà avec le domaine pour la 1
f(x) = x(Vx + 1)³
Df = R+ (et pas R*+)
f'(x) = (Vx + 1)³ + 3x.(Vx + 1)²/(2Vx)
f'(x) = (Vx + 1)³ + (3/2).Vx.(Vx + 1)²
f'(x) = (Vx + 1)² * [(Vx + 1) + (3/2).Vx]
f'(x) = (Vx + 1)² * ((5/2).Vx + 1)
f'(x) = (1/2).(Vx + 1)² * (5Vx + 2)
Df' = R+
:zen:
Bonjour, merci.
Je ne comprend pas déjà le domaine de déf. Pourquoi R+ ?
Je ne comprend pas non plus le passage à la 2ème ligne. Pour (3/2)Vx.(Vx+1)².
Et ni les 2 dernières lignes...? :mur:
Pour [(Vx+1)+(3/2)Vx], je trouve (4/2)Vx+1 ? :hum:
Et la dernière ligne .... ???
C'est que des problèmes de calculs ! J'ai vraiment des lacunes...
Merci pour votre aide.
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 21 Avr 2014, 13:15
par paquito » 21 Avr 2014, 13:15
Snailfire a écrit:Bonjour, merci.
Je ne comprend pas déjà le domaine de déf. Pourquoi R+ ?
Je ne comprend pas non plus le passage à la 2ème ligne. Pour (3/2)Vx.(Vx+1)².
Et ni les 2 dernières lignes...? :mur:
Pour [(Vx+1)+(3/2)Vx], je trouve (4/2)Vx+1 ? :hum:
Et la dernière ligne .... ???
C'est que des problèmes de calculs ! J'ai vraiment des lacunes...
Merci pour votre aide.
En fait il apparaît x/Vx, qui se simplifie en Vx et Vx n'est plus en dénominateur, donc f'(0) est calculable.
Sinon, ce n'est que du calcul.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
