Narration de recherche - Géométrie

[Walter White]

Bien le bonjour,

On m'a donné une narration recherche, un exercice tout droit sorti des bureaux de l'IREM de Montpellier qui décrit ça comme une activité qui «consiste à proposer aux élèves de travailler sur un problème choisi hors de toute contrainte de programme, puis de rédiger un compte rendu de leur recherche qui décrive toutes les idées, toutes les pistes suivies, y compris celles qui n’ont pas abouti.»


Aimant bien la réflexion dans les maths, la recherche et n'aimant pas appliquer bêtement ce qu'on me donne, j'apprécie grandement un tel exercice. Je viens cependant demander quelques conseils et pistes ici, sait-on jamais. J'ai en fait assez peur de ne pas suivre assez de pistes, de pas bien expliquer mon raisonnement ou de tout simplement n'en avoir pas (de raisonnement).

Voici la narration de recherche en question : http://image.noelshack.com/fichiers/2014/13/1395842105-narration-de-recherche.jpg

J'ai commencé en faisant un carré, je constante qu'il y a 6 segments possibles avec 4 points, avec 5 points, 4 segments possible (si ils sont tous reliés donc «joignant deux à deux chacun des points»), avec 6 points 5 segments possibles.

Enfin, j'ai commencé par illustrer ceci en faisant une figure géogebra et en mettant les segments (j'ai utilisé l'outil polygone pour les colorer et les faire ressortir, je voyais pas comment autrement).

ICI : http://www.noelshack.com/2014-13-1395843201-narration-de-recherche-2.jpg

Mais maintenant je suis un peu perdu, je ne sais pas trop comment procéder, surtout qu'il me faut mettre ma propre pensée en contradiction pour avancer, etc.

[Monsieur23]

Aloha,

Tu as dû te tromper pour 5 et 6 points (tu as forcément plus de segment avec 5 points qu'avec 4…)

[Walter White]

C'est vrai, mais est-ce que je dois faire tous les segments possibles OU tous les segments possibles à partir d'un seul point, Si j'ai ABCD je peux faire à partir de A seulement 3 segments, mais si je compte tous ceux qu'il y a (AB, AC, BC, BD...) il y a plus que trois.

Lequel des deux cas est celui du devoir ?

[Monsieur23]

Je pense qu'on veut tous les segments, entre tous les points. Sinon, avec trois points, tu n'aurais que 2 segments.

[capitaine nuggets]

Salut !

Voici quelque pistes que j'explorerais :+++:

- Avant toute chose, tu peux commencez par étudier les premiers cas N=2,3,4,5,6... puis éventuellement, formuler une conjecture.
- Si on note N_n le nombre de segments qu'il est possible de former avec n points, n>1, que se passe-t-il si on rajoute un point supplémentaire ? Autrement dit, essaie d'exprimer en fonction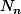
- Si on réfléchi bien, le but est de former différent segment en reliant deux points, donc cela revient à choisir des couples de points. Ainsi, on ne serait plus amener à compter le nombre de segments possibles mais le nombre de couples de points différents qu'il est possible de prendre (en faisant attention : par exemple (A,B) et (B,A) déterminent-ils le même segments ?).
- Une remarque géométrique. On considère des points quelconque, donc rien ne t'interdit de les disposer d'une certaines manière pour faciliter les chose sans perdre la généralité :+++:

[Ben314]

Salut,
1) Une remarque :
Il manque le segment DF sur ta figure Géogébra

2) Une autre piste possible (vu que tu en veut des tas...) :
S'il y a n points sur le dessin, de chaque point du dessin, il "part" combien de segments ?
Peut on en déduire quelque chose ?

[Walter White]

Je pense qu'on veut tous les segments, entre tous les points. Sinon, avec trois points, tu n'aurais que 2 segments.

Ok, alors ça me donne : avec 2 points = 1 segment ; 3 points = 3 segments ; 4 points = 6 segments ; 5 points = 10 segments ; 6 points = 15 segments.

- Si on note N_n le nombre de segments qu'il est possible de former avec n points, n>1, que se passe-t-il si on rajoute un point supplémentaire ? Autrement dit, essaie d'exprimer N_{n+1} en fonction N_n

J'ai pas compris cette question, enfin, c'est N + [un point en plus] et donc N + [x segments en plus] ?

Dans ce cas la, N_n = N+x (x segments). Mais le nombre n'est pas constant.

- Une remarque géométrique. On considère des points quelconque, donc rien ne t'interdit de les disposer d'une certaines manière pour faciliter les chose sans perdre la généralité

J'ai pensé à un cercle...

[beagle]

Bon l'idée c'est que tu patauges le plus longtemps possible,
et que tu expliques pourquoi tu te gourres
pourquoi c'est compliqué
tu n'es pas noté sur le résultat, mais sur ton analyse de tes erreurs.
donc le mieux serait de te gourrer exprès, en sachant où tu te gourres et pourquoi,
et comme cela après tu peux rectifier tout seul.

vers la fin, tu dis bon c'est pas un exo de géométrie puisque je dois tout dénombrer,
c'est donc un exo de rangement,
donc faut ranger tes segments dans une boite.
chaque segment peut se décrire par les deux points du segments
A et B
ou bien tu peux appeler le premier point 1, le deuxième 2, ...
alors range tes segments dans une boite carrée
ABCDEFG ou 123456789 colonnes
A
B
C
D
ou
1
2
3
4
5
rangées
note dans une case les segments AF pour rangée A et colonne F

enfin tu te débrouilles pour ranger tes segment avant de passer à table,
on ne sera pas toujours là pour ramasser tes segments ...

et après tu compteras quand ce sera bien ranger...

[Walter White]

tu n'es pas noté sur le résultat, mais sur ton analyse de tes erreurs.
donc le mieux serait de te gourrer exprès, en sachant où tu te gourres et pourquoi,
et comme cela après tu peux rectifier tout seul.

Ouais, je comptais faire ça, mais je pense compter sur moi pour me gourer vraiment en fait.

[capitaine nuggets]

J'ai pas compris cette question, enfin, c'est N + [un point en plus] et donc N + [x segments en plus] ?

Dans ce cas la, N_n = N+x (x segments). Mais le nombre n'est pas constant.

Soit un ensemble de points distincts deux à deux et posons le nombre de segments qu'il est possible de former avec ses points (Attention aux cas particulier : ne désigne pas un segment et ).
Supposons connu. Considérons un -ième point distincts de ceux de et considérons alors l'ensemble .
Peut-on essayer exprimer le nombre de segments qu'il est possible de former avec ses points sachant qu'on connait le nombre de segment qu'on peut former avec n d'entre eux ? Autrement dit, peut-on exprimer en fonction de ?

J'ai pensé à un cercle...

Oui, ça peut servir (au moins on est sûr qu'il ne seront pas alignés :++:)
Tu peux utiliser cette représentation pour ce que je t'ai proposé plus haut :
Supposons qu'on a n points sur un cercle et qu'on connaisse le nombre de segment qu'on peut former entre tout ces points, qu'advient-il de ce nombre si on ajoute un point extérieur au cercle ?
(extérieur pour mieux se représenter la chose ^^).

[beagle]

Ouais, je comptais faire ça, mais je pense compter sur moi pour me gourer vraiment en fait.

bah, c'est facile, en dénombrement,
soit tu en oublies, donc trouve des manières de compter ou tu oublies certains segments,
soit tu en comptes en trop, certains sont comptés deux fois, ben trouve le moyen d'en compter deux fois,
puis vers la fin ni trop ni trop peu, pile poil...

[Walter White]

Soit un ensemble de points distincts deux à deux et posons le nombre de segments qu'il est possible de former avec ses points (Attention aux cas particulier : ne désigne pas un segment et ).
Supposons connu. Considérons un -ième point distincts de ceux de et considérons alors l'ensemble .
Peut-on essayer exprimer le nombre de segments qu'il est possible de former avec ses points sachant qu'on connait le nombre de segment qu'on peut former avec n d'entre eux ? Autrement dit, peut-on exprimer en fonction de ?

D'acooord ! Je pense qu'on aura autant de possibilités de segments qu'on aura de points (+ on rajoute les segments qui sont déjà formés par les points précédents)


Ainsi on a tous les points d'avant et les nouveaux segments formés par le nouveau point et tous les autres points.

Je sais pas si j'ai bien compris et été compris...

[Ben314]

Je persiste à penser que, de compter combien de segments "partent" de chacun des points, c'est... plus joli... comme méthode.

[Robic]

Pareil.

Par exemple j'ai n points. Prenons-en un au hasard. Je peux tracer [censuré] segments partant de ce point. Et comme il y a n points, ça fait au total n*[censuré] segments. Génial, l'exercice est fini, trop fastoche !

Ah mais non, ça ne marche pas ! (On s'en rend compte en comparant la formule avec les cas particuliers étudiés au début.) Et là il faut chercher pourquoi, et je pense qu'il y a de quoi raconter. Une fois qu'on a compris pourquoi ça ne marche pas, on pourra corriger la formule et obtenir la bonne.

[Walter White]

Pareil.

Par exemple j'ai n points. Prenons-en un au hasard. Je peux tracer [censuré] segments partant de ce point. Et comme il y a n points, ça fait au total n*[censuré] segments. Génial, l'exercice est fini, trop fastoche !

Ah mais non, ça ne marche pas ! (On s'en rend compte en comparant la formule avec les cas particuliers étudiés au début.) Et là il faut chercher pourquoi, et je pense qu'il y a de quoi raconter. Une fois qu'on a compris pourquoi ça ne marche pas, on pourra corriger la formule et obtenir la bonne.

Je peux tracer (n-1) segments partant de ce point car on enlève le point duquel on part [(mais après il y a aussi les segments entre eux!) Je parle des segments entre eux parce que pour N=4 points, on a les "liaisons" AB,AC,AD,BD,BC,CD) Donc il n'y a pas que "partant de ce point" ?! ]

Et comme il y a n points ça fait n(n-1) segments.

C'est ce qu'on est censés trouver logique et qui en fait ne marche pas ?
Je suis paumé je crois...

[Robic]

Et comme il y a n points ça fait n(n-1) segments.

Tout à fait !
Maintenant calcule n(n-1) pour les n que tu as déjà étudiés (de 2 à 6 je crois - cela dit les valeurs pour 5 et 6 sont fausses dans ton premier message, je suppose que tu as corrigé (*)). Tu remarqueras que ce n'est pas la même chose, mais il y a quand même un point commun... En comparant avec le cas n=2 ou le cas n=3, tu devrais comprendre ce qui se passe.

-----
(*)
Pour n = 4 : 4 côtés + 2 diagonales = 6 segments.
Pour n = 5 : 5 côtés + 5 diagonales = 10 segments.
Pour n = 6 : 6 côtés + 3 diamètres + 6 "diagonales pas diamètres" = 15 segments.

[beagle]

Je persiste à penser que, de compter combien de segments "partent" de chacun des points, c'est... plus joli... comme méthode.

je persiste à penser que le point n'est pas le segment,
que le segment est bien mieux représenté par une case = les deux points, un couple
et que donc de compter les cases est bien plus joli...logi...

[Miguelito]

Tu as presque trouvé. Ta formule est n*(n-1), pourquoi ça ne marche pas? si tu raisonnes sur trois points A,B,C les segments sont AB, AC, BA, BC, CA, CB ce qui te donne 3*2 = 6 mais tu as compté deux fois les segments AB et BA, AC et CA, BC et CB si tu divises par 2 tu trouves 6/2=3, pour 4 points 4*3/2=6, ....
Un autre raisonnement: tu dis que tu as x segments pour N points et tu ajoutes un point duquel tu peux faire partir N segments au total tu as x+N segments par récurrence tu vois que pour N+1 points le nombre de segments est: 1+2+3+.....+(N-1) c'est à dire (N-1)*(N-1+1)/2

[beagle]

Je persiste à penser que, de compter combien de segments "partent" de chacun des points, c'est... plus joli... comme méthode.

Bon, c'est de la narration, faut que cela soit un peu narrant.faut des rebondissements...
Alors j'ai changé d'idée, c'est la méthode de Ben314 qui est la plus économique, donc la plus esthétique.
Mais ce type est énervant d'avoir raison, donc tu dis au prof que tu n'as suivi sa méthode qu'après avoir trouvé la tienne.
c'est ça la narration...
situations initiale
péripéties
dénouement

Bon de chaque point il part (n-1) segments.
il y a n points,
il part donc n x (n-1) segments
Voila c'était pas compliqué.
Comment ça il y a un problème, c'est quoi le problème?
On les a tous, bon peut-ètre un peu trop mème,
bon, ben échange les doublons sur le web, et fais toi du blé...
allez narre...

[capitaine nuggets]

Soit un ensemble de points distincts deux à deux et posons le nombre de segments qu'il est possible de former avec ses points (Attention aux cas particulier : ne désigne pas un segment et ).

D'ailleurs, on peut même voir rapidement le nombre de segments qu'on peut former avec les éléments de : Il suffit de faire un tableau où on met les points en ligne et en colonne et dans chaque case, on écrit le segment formé par ces couples de points :

Exemple pour :
[CENTER]
[/CENTER]

On observe que les termes diagonaux et ne sont pas des segments !
Enfin, les éléments en-dessous de la diagonale sont exactement les mêmes que ceux qui sont au-dessus.

:+++: