Dénombrer, cardinaux

[Lostounet]

Bonjour,

Je suis nul en dénombrement.
Je dois rendre l'exercice suivant:

1. Calculer la somme des cardinaux de toutes les parties d'un ensemble fini E à n éléments

2. Soit F une partie de E de cardinal k. Montrer que le nombre de couples (X,Y) de P(E)^2 vérifiant
est

En déduire que:

Pour la question 1:

Soit E un ensemble fini à n éléments. On note, pour k dans , les parties
à k éléments.

On souhaite donc calculer la somme des éléments de tous les que l'on peut former à partir des n éléments de E.

Il s'agit donc de la somme:


Somme que je sais calculer.

Merci de m'aider pour la 2

[busard_des_roseaux]

bonjour,

sans tenir compte des éléments de F, on dit qu'il y a
ensembles de la forme chacun de cardinal c+k

Pour déterminer un couple X,Y, on se demande combien X a d'élements (hormis ceux de F) et Y en a alors le complémentaire (on partage en fait le nombre c d'élements en et )



on somme sur c pour les différentes possibilités de \ F

d'où

[Maxmau]

Bonjour,

Je suis nul en dénombrement.
Je dois rendre l'exercice suivant:

1. Calculer la somme des cardinaux de toutes les parties d'un ensemble fini E à n éléments

2. Soit F une partie de E de cardinal k. Montrer que le nombre de couples (X,Y) de P(E)^2 vérifiant
est

En déduire que:

Pour la question 1:

Soit E un ensemble fini à n éléments. On note, pour k dans , les parties
à k éléments.

On souhaite donc calculer la somme des éléments de tous les que l'on peut former à partir des n éléments de E.

Il s'agit donc de la somme:


Somme que je sais calculer.

Merci de m'aider pour la 2

bonjour
pour la 2/ traite d'abord le cas k=0 c'est à dire F vide en remarquant que
se donner (X,Y) ds P(E)^2 tq X inter Y = vide revient à se donner une application de E ds un ensemble à 3 éléments {1,2,3}
le cas général s'en déduit tout de suite

[busard_des_roseaux]

des idées pour la fin, je trouve une formule différente de celle de l'énoncé ?

[Lostounet]

Désolé, mais je ne comprends pas très bien les deux méthodes :(

Pour busard, pour reprendre un peu, si je considère que X possède i éléments, et X inter Y = F possède k éléments, X privé de l'intersection possède i - k éléments...

..?

Pour Maxmau, pourrais-tu expliciter cette application?

[Ben314]

Non, l'énoncé est correct.

Vu le "en déduire", on attend que tu scinde la somme en fonction de l'ensemble :

car il y a partie de à éléments.

Sinon, il y a une autre méthode plus rigolote et plus rapide en utilisant la bijection triviale entre et

[Lostounet]

Non, l'énoncé est correct.
Vu le "en déduire", on attend que tu scinde la somme en fonction de l'ensemble :

car il y a partie de à éléments

[Ben314]

:cry:

??????????

[busard_des_roseaux]

@lostounet: on fixe k provisoirement.
on pose qu'on éclate en pour card(X-F)et pour card(Y-F)

[Lostounet]

ça va pour la deuxième égalité, mais la première je ne vois pas comment scinder la somme :/


Les maths, c'est vraiment pas pour tout le monde x)
J'aurais du me contenter de mon Bac

[busard_des_roseaux]

ah oui, d'accord, j'avais oublié de faire varier le k de card(F), il me manquait un facteur

[Maxmau]

Désolé, mais je ne comprends pas très bien les deux méthodes

Pour busard, pour reprendre un peu, si je considère que X possède i éléments, et X inter Y = F possède k éléments, X privé de l'intersection possède i - k éléments...

..?

Pour Maxmau, pourrais-tu expliciter cette application?

Si X inter Y est vide tu considères l'application f de E dans {1,2,3} tq:
f(t) =1 si t dans X, f(t) =2 si t dans Y et f(t) = 3 si t n'est ni ds X ni ds Y.
Réciproquement une application de E ds {1,2,3} est du type précédent.
le nombre de ces applications est 3^n.
La généralisation est immédiate

[Ben314]

ça va pour la deuxième égalité, mais la première je ne vois pas comment scinder la somme :/

Ça c'est des problèmes de compréhension du symbole "sigma" (archi classique).
Si tu as une somme, par exemple S=a+b+c+d+e+f+g+h+i+j+k, tu peut la calculer comme tu veut, par exemple en disant que S=(g+k+b)+(f+j+h+a)+(i+d+c+e) : le tout, c'est de faire gaffe à prendre tout les éléments une fois et une seule.
Dans la somme en question qui porte sur toutes les parties X et Y de E, j'ai juste rajouté des "parenthèses" pour grouper ensemble les termes qui donnent la même intersection pour X et Y. Le truc qu'on somme, à savoir le card(X inter Y) n'a absolument aucune importance ici : on ne fait que le recopier.

Si tu veut une écriture "théorique" de ce que je raconte, ça consiste à dire que, si est une partition d'un ensemble alors . Et ce n'est pas un "théorème", mais juste le fait qu'une somme ça se fait dans l'ordre qu'on veut...

[Ben314]

Sinon, pour le 2), la façon plus maline de le faire, c'est d'utilise le fait que le cardinal d'un ensemble, la somme 1+1+1...+1 avec un 1 pour chaque élément de l'ensemble, c'est à dire en "propre" où vaut si et sinon (fonction indicatrice de )

d'où





Or, pour fixé compte le nombre de couple de parties telles que appartienne à et à et, clairement, le nombre de parties contenant est
d'où le résultat.

[Sourire_banane]

Les maths, c'est vraiment pas pour tout le monde x)
J'aurais du me contenter de mon Bac

Je sais que c'est pas l'endroit mais c'est le moment de te botter le cul en ligne, lol
"Les maths c'est pas pour tout le monde" blah blah n'importe quoi. La première année peut être dure d'autant plus que tu es quand même dans une très bonne prépa. Mais ça c'est le choc thermique je dirais. Une fois que t'auras saisi le rythme de travail, et que tu auras assimilé TA bonne façon de travailler, la bonne façon de faire tes exos, ça coulera mieux !
Allez, courage, personne n'a dit que la prépa c'est facile, mais tu seras d'autant plus méritant si tu réussis à continuer

[busard_des_roseaux]

Je suis nul en dénombrement.

bonsoir,

quelques propriétés

à la réunion disjointe, correspond l'addition des cardinaux
au produit cartésien, correspond la multiplication des cardinaux
Quand les cas sont "indépendants" , on les liste sous forme d'un produit cartésien
ou d'une réunion disjointe de tels produits.

enfin tu as le principe des bergers, quand on dispose d'une application surjective
si les fibres ont toutes le même cardinal
alors

[Lostounet]

enfin tu as le principe des bergers, quand on dispose d'une application surjective
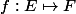
si les fibres ont toutes le même cardinal
alors

Oui le lemme des bergers ! On l'a vu en cours.

Je sais que c'est pas l'endroit mais c'est le moment de te botter le cul en ligne, lol
"Les maths c'est pas pour tout le monde" blah blah n'importe quoi. La première année peut être dure d'autant plus que tu es quand même dans une très bonne prépa. Mais ça c'est le choc thermique je dirais. Une fois que t'auras saisi le rythme de travail, et que tu auras assimilé TA bonne façon de travailler, la bonne façon de faire tes exos, ça coulera mieux !
Allez, courage, personne n'a dit que la prépa c'est facile, mais tu seras d'autant plus méritant si tu réussis à continuer

Le problème, c'est que je n'arrive à faire quasiment aucun exercice...
Je commence à avoir une phobie des maths, je t'assure. :ptdr:


@Ben: Je comprends le principe des sommes imbriquées. Le problème, c'est que je n'arrive pas à voir tout ça sur le diagramme de Venn.

Ce serait vraiment bien si vous pouviez reprendre à zéro :/ J'ai vraiment essayé mais je ne comprends pas. Je vais essayer de reformuler autrement ce que j'ai compris des posts précédents..

On veut déterminer le nombre de couples (X,Y), tel que leur intersection soit à k éléments.
Si je fixe X, à x éléments par exemple, X strict comporte (x - k) éléments.

Combien de X est-ce que je peux former ? Combien d'ensembles à (x - k) éléments puis-je former lorsque E (ensemble total) contient n éléments...?
C'est justement

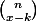
Ensuite pour chaque X, il y a un Y qui lui correspond .. C'est bon pour le raisonnement .. après..

[Ben314]

Non, déjà, ça déconne :
je suppose que ton "X strict", ça veut dire X privé de F : comme X doit obligatoirement contenir F, ç'est pas la peine de tenir compte des éléments de F dans le calcul du nombre de X.
Sauf que justement, ça veut dire que les x-k autres éléments de X (où x=card(X)) tu les prend pas n'importe où des E, mais dans E privé de F ce qui te fait binom(n-k,x-k) possibilités.

[busard_des_roseaux]

Je suis nul en dénombrement.

1. Calculer la somme des cardinaux de toutes les parties d'un ensemble fini E à n éléments


Soit E un ensemble fini à n éléments. On note, pour k dans , les parties
P_k (E) à k éléments.

ta pensée est un peu confuse: il y a une hésitation , on ne sait pas si P_k(E) désigne une partie (générique, quelconque) de E ou bien la collection de toutes les parties de E
qui ont précisemment k éléments.
En fait c'est l'option (2) et ce qui sert, c'est que cette collection de parties
est de cardinal binom(k;n).



On souhaite donc calculer la somme des cardinaux des éléments de
Il s'agit donc de la somme:

....................................................