J'étudie le test du khi-deux en autodidacte et je me suis fait un petit programme qui me fait tous les calculs.
Je me pose le problème suivant:
Un prof rend une interro à ses 30 élèves.
- 20 d'entre eux ont obtenu 10/20
- 5 d'entre eux ont obtenu 11/20
- 5 d'entre eux ont obtenu 9/20.
Je me demande si on peut considérer qu'il y a là une répartition uniforme, c'est-à-dire si on peut penser que tous les élèves ont obtenu la même note.
Voici ce que me répond mon programme:
Khi carré
=((5-10)² / 10) +((20-10)² / 10) +((5-10)² / 10)
=(-5² / 10) +(10² / 10) +(-5² / 10)
=(25/10) + (100/10) + (25/10)
=2.5 +10 +2.5
15
Khi2_observé=15.0000
Valeur à ne pas dépasser=0.1026 (calculée en fonction de la précision souhaitée: 95%)
On NE PEUT donc PAS assimiler cette distribution à une distribution de Uniforme avec une précision de 95%
Je suis surpris par la sévérité du test mais je me demande aussi si j'avais le droit de faire ce test avec seulement 3 classes et 30 observations. Qu'en pensez-vous ?
Test du khi-deux
7 messages
- Page 1 sur 1
Eh ma foi, c'est vrai ce que tu dis là ! Ce sont les effectifs qui doivent se ressembler et non les valeurs. Donc ma répartition n'est absolument pas une répartition uniforme et le test du khi-deux a bien raison de me répondre par un gros NON.
Ceci dit, avais-je le droit de tenter le test avec de si petits effectifs ?
Par ailleurs, si je dis que 4 élèves et non 5 ont obtenu les notes 9 et 11, alors le test du khi-deux m'oblige à rattacher ces classes de 4 éléments à la classe la plus proche. J'aboutis donc à une classe unique avec un effectif de 28 et mon programme me dit:
Khi carré
=((28-28)² / 28)
=(0² / 28)
=(0/28)
=0
0
Khi2_observé=0.0000
Valeur à ne pas dépasser=99999.0000 (calculée en fonction de la précision souhaitée: 95%)
On PEUT donc assimiler cette distribution à une distribution de Uniforme avec une précision de 95%
Là, je trouve le test trop généreux. Avais-je le droit de le tenter ? (Je pose peut-être des questions un peu simplettes, mais quand on bosse seul pour étudier un sujet, on se pose des tas de questions. Plus tard, ça me paraîtra peut-être évident, mais pour l'instant, j'ai besoin d'aide)
Ceci dit, avais-je le droit de tenter le test avec de si petits effectifs ?
Par ailleurs, si je dis que 4 élèves et non 5 ont obtenu les notes 9 et 11, alors le test du khi-deux m'oblige à rattacher ces classes de 4 éléments à la classe la plus proche. J'aboutis donc à une classe unique avec un effectif de 28 et mon programme me dit:
Khi carré
=((28-28)² / 28)
=(0² / 28)
=(0/28)
=0
0
Khi2_observé=0.0000
Valeur à ne pas dépasser=99999.0000 (calculée en fonction de la précision souhaitée: 95%)
On PEUT donc assimiler cette distribution à une distribution de Uniforme avec une précision de 95%
Là, je trouve le test trop généreux. Avais-je le droit de le tenter ? (Je pose peut-être des questions un peu simplettes, mais quand on bosse seul pour étudier un sujet, on se pose des tas de questions. Plus tard, ça me paraîtra peut-être évident, mais pour l'instant, j'ai besoin d'aide)
Bon, ben déjà, cette phrase là :
je crois que ça montre qu'il faudrait un peu revoir le vocabulaire des proba...Frede a écrit:Je me demande si on peut considérer qu'il y a là une répartition uniforme, c'est-à-dire si on peut penser que tous les élèves ont obtenu la même note.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Une petite question un peu bête en fait : De quel type de test de Khi - deux il s'agit exactement ?, parce que il y'a plusieurs type de tests de Khi - deux sur quel on tombe. Je revois à l'instant mes anciens cours de statistique, et je trouve qu'il y'a par exemple : test d'adéquation à une loi ou bien test dhomogénéité ou bien test d'indépendance de deux caractères... etc Le quel exactement ?
Merci d'avance.
Merci d'avance.
Merci pour ces deux réponses. Ce sont de bonnes questions que vous me posez là.
Pour ce que dit Ben, pas de problème: j'étais parti sur une idée fausse car je voyais la répartition uniforme de façon plutôt intuitive: répartition uniforme= tout le monde est à égalité. J'avais oublié que c'était égalité de chances au départ (comme les 6 faces d'un dé) et non égalité dans la prestation. Mais bon, c'est noté maintenant, je ne m'y tromperai plus.
Ce que dit Barbu me donne une info que j'ai peut-être lue quelque part mais que j'ai sans doute oubliée aussitôt: il y a plusieurs variétés de test du khi2. L'essai que j'ai fait relevait bien sûr de l'adéquation à une loi. C'est le type de test le plus fréquent dans le livre que j'utilise ("Stats et probas pour écoles vétérinaires", on a les livres qu'on peut, j'ai eu celui-là pour une bouchée de pain dans une brocante. Je le trouve très bien mais peut-être un peu superficiel). Barbu, si tu peux me dire ce qui différencie, ces 3 types de khi2, ça m'intéresse. Je pense que les calculs sont les mêmes (ne me dis pas le contraire, ça m'obligerait à revoir mon programme !) mais peut-être l'approche est-elle différente.
Ce qui m'inquiète le plus, c'est que je ne voudrais pas faire de test dans des cas où je n'en ai pas le droit. En avais-je le droit pour les essais que j'ai fait ? Je pense qu'on peut tester l'adéquation à la loi uniforme pour des lancers à pile ou face, donc avec 2 classes seulement. Par contre 30 valeurs, c'est peut-être un peu léger.
Toute info sur le khi-deux est bienvenue. Je vous mets dans la confidence: j'envisage d'envoyer mon programme à un autre Forum ("Codes-sources") et il vaudrait donc mieux qu'il n'y ait pas trop d'erreurs.
Pour ce que dit Ben, pas de problème: j'étais parti sur une idée fausse car je voyais la répartition uniforme de façon plutôt intuitive: répartition uniforme= tout le monde est à égalité. J'avais oublié que c'était égalité de chances au départ (comme les 6 faces d'un dé) et non égalité dans la prestation. Mais bon, c'est noté maintenant, je ne m'y tromperai plus.
Ce que dit Barbu me donne une info que j'ai peut-être lue quelque part mais que j'ai sans doute oubliée aussitôt: il y a plusieurs variétés de test du khi2. L'essai que j'ai fait relevait bien sûr de l'adéquation à une loi. C'est le type de test le plus fréquent dans le livre que j'utilise ("Stats et probas pour écoles vétérinaires", on a les livres qu'on peut, j'ai eu celui-là pour une bouchée de pain dans une brocante. Je le trouve très bien mais peut-être un peu superficiel). Barbu, si tu peux me dire ce qui différencie, ces 3 types de khi2, ça m'intéresse. Je pense que les calculs sont les mêmes (ne me dis pas le contraire, ça m'obligerait à revoir mon programme !) mais peut-être l'approche est-elle différente.
Ce qui m'inquiète le plus, c'est que je ne voudrais pas faire de test dans des cas où je n'en ai pas le droit. En avais-je le droit pour les essais que j'ai fait ? Je pense qu'on peut tester l'adéquation à la loi uniforme pour des lancers à pile ou face, donc avec 2 classes seulement. Par contre 30 valeurs, c'est peut-être un peu léger.
Toute info sur le khi-deux est bienvenue. Je vous mets dans la confidence: j'envisage d'envoyer mon programme à un autre Forum ("Codes-sources") et il vaudrait donc mieux qu'il n'y ait pas trop d'erreurs.
Il s'agit de faire un test du Khi deux d'adéquation. Sous lhypothèse H_0 que la loi est uniforme sur {9,10,11} les effectif attendus sont de 10 pour chaque classes. Et le nombre de dégrées de liberté est de: n-1 = 2
La statistique de test est:
^2}{E_i})
où:
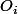 est l'effectif observé pour la classe i
est l'effectif observé pour la classe i
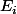 est l'effectif attendu pour la classe i
est l'effectif attendu pour la classe i
(Bien sur si l'on prend pour H_0 lhypothèse que la loi est uniforme sur {0, 0.5, 1 , 1.5, .... , 19, 19.5, 20} le test donnera un résultat très différent )
A noter que le test du Khi deux d'adéquation est différent du test du test du Khi deux d'indépendance car chacun adresse une situation différente. ( Le test du Khi deux d'indépendance permet de tester si les lignes et les colonnes dun tableau sont indépendantes )
La statistique de test est:
où:
(Bien sur si l'on prend pour H_0 lhypothèse que la loi est uniforme sur {0, 0.5, 1 , 1.5, .... , 19, 19.5, 20} le test donnera un résultat très différent )
A noter que le test du Khi deux d'adéquation est différent du test du test du Khi deux d'indépendance car chacun adresse une situation différente. ( Le test du Khi deux d'indépendance permet de tester si les lignes et les colonnes dun tableau sont indépendantes )
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
