Zeros triviaux !

par **barbu23** » 09 Fév 2009, 19:34

Bonsoir :
Que signifie un zero trivial de la fonction zeta de Riemann :

Quelle différence y'a-t-il entre zero trivial et un zero non trivial de la fonction zeta de Riemann ?
Merci infiniment !

par **Nightmare** » 09 Fév 2009, 19:37

Salut :happy3:

On parle abusivement des zéros triviaux de la fonction zeta de Riemann mais ceux-ci se réfèrent plutot à son prolongement analytique sur

.

Les zéros triviaux sont alors les -2k avec k naturel.

par **Nightmare** » 09 Fév 2009, 19:44

J'ai pas répondu à la deuxième question.

Les -2k sont des zéros triviaux parce qu'ils apparaissent trivialement comme des zéros (à la vue d'une équation fonctionnelle satisfaite par zeta par exemple).

Cependant elle possède d'autres zéros qu'on ne sait a priori pas déterminer. Riemann a cependant émit l'hypothèse qu'ils étaient tous de la forme

. A démontrer...

par **barbu23** » 09 Fév 2009, 19:45

Salut "Nightmarre" :
Par exemple, pour :

,

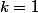
, et

( ce n'est pas evident du tout )
tu peux m'expliquer pourqui ?
Merci infiniment !

par **ThSQ** » 09 Fév 2009, 19:50

On peut prolonger la fonction zeta sur C\{1}, c'est de ce prolongement dont il est question.

par **Nightmare** » 09 Fév 2009, 19:58

Comme je te l'ai dit et le répète ThSQ, la définition mettant en jeu la série

n'est valable que pour un complexe de partie réelle supérieure à 1. On prolonge analytiquement la fonction pour pouvoir la calculer pour tout complexe différent de 1. On peut alors la définir par une intégrale ou une équation fonctionnelle, mais bien sur on ne peut plus la définir par la série du début.

par **barbu23** » 09 Fév 2009, 20:10

Svp, je comprends pas enocre cette question sur les zeros triviaux, :briques: :marteau: relisez svp ce que j'ai écrit dans l'autre poste çi dessus, et expliquez moi ce la methode de calcul svp !
Merci infiniment !

par **SimonB** » 09 Fév 2009, 20:18

barbu23 a écrit:Salut "Nightmarre" :
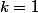
Par exemple, pour : , , et ( ce n'est pas evident du tout )
tu peux m'expliquer pourqui ?
Merci infiniment !

Ta série diverge trivialement...

Relis donc ce qu'ont écrit ThSQ et Nightmare : il s'agit d'un prolongement de la fonction zeta telle qu'elle a été définie sur les complexes de partie réelle supérieure à 1 à tout le plan complexe moins 1, de sorte à rendre ce prolongement analytique.

par **kazeriahm** » 09 Fév 2009, 20:46

wikipedia est ton ami http://fr.wikipedia.org/wiki/Fonction_Zeta_de_Riemann#.C3.89quation_fonctionnelle

par **gaye moussa** » 08 Oct 2013, 20:39

j' ai une idee visant a infirmer l'hypothese de Riemann les zeros non triviaux sont tous imaginaires purs et leurs parties imaginaires sont negatives

Zeros triviaux !

Zeros triviaux !

Qui est en ligne