Zéros communs de polynômes

[Nightmare]

Salut à tous :happy3:

Je vous propose cet exercice, je n'ai qu'une résolution partielle, j'attends de voir vos démonstrations.

On considère k polynômes quelconques de de sorte que la somme de leur degré n'excède pas n.

Montrer que p divise le nombre de zéros communs aux k polynômes.

Bon courage.

:happy3:

[Nightmare]

J'ai réussi à compléter ma preuve pas si difficile que ça finalement.

Cet exercice admet une très belle application dans le cas où l'on prend des polynômes de valuation non nulle.

[Nightmare]

Bon en fait je n'ai pas réussi à conclure. Voici comment j'ai raisonné :

Je note les k polynômes et E l'ensemble de leurs zéros communs.

Ma première idée était de chercher à exprimer card(E) correctement. J'ai cherché alors un polynôme qui prendrait la valeur 1 en tous les élément de E et 0 autrement.

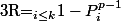D'après le petit théorème de Fermat, le polynôme convient et le cardinal de E est alors égal à la somme des images des éléments de par R.

Il faudrait donc montrer que cette somme est nulle. Je pensais avoir réussi mais je n'y arrive pas. Je ne vois pas comment utiliser l'hypothèse sur la somme des degrés ...

Une idée?

[Nightmare]

En gros, !

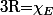
[skilveg]

Salut,

Ton idée est excellente! Ce que tu peux faire à partir de là c'est développer ta "fonction indicatrice" en combinaison linéaire de monômes, et regarder ce qui se passe quand tu sommes un de ces monômes sur , avec l'hypothèse sur le degré.

Le théorème que tu essaies de démontrer s'appelle théorème de Chevalley-Warning, pour info. La preuve que tu es en train de trouver est entre autres dans le livre d'arithmétique de J.-P. Serre; il y en a une autre un peu différente dans le bouquin de Ireland et Rosen.

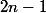
Un joli résultat qui peut être prouvé avec ce théorème: prends entiers naturels. Alors tu peux toujours en choisir dont la somme soit divisible par .