Urgent
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AHLEM
- Messages: 1
- Enregistré le: 15 Aoû 2010, 23:27
-
 par AHLEM » 15 Aoû 2010, 23:59
par AHLEM » 15 Aoû 2010, 23:59
Resoudre cette formule
/2>(sinx+siny)/2)
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 16 Aoû 2010, 07:38
par Finrod » 16 Aoû 2010, 07:38
J'ai déplacé la discussion vers un forum plus adapté.
Il est demandé d'être plus prolixe en matière d'explications ou éventuellement de politesse.
SI le 1/2 es dans le sinus à gauche, alors c'est une inégalité de concavité.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 16 Aoû 2010, 12:33
par Ericovitchi » 16 Aoû 2010, 12:33
une inégalité de concavité qui n'est donc vrai qu'aux endroits où le sinus est concave, et donc pas partout :

Voici les zone (x,y) dans lesquelles l'inégalité est vérifiée.
 par busard_des_roseaux » 16 Aoû 2010, 17:23
par busard_des_roseaux » 16 Aoû 2010, 17:23
busard_des_roseaux a écrit:Bonjour,
poser à droite
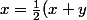+{1 \over 2}(x-y))
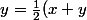-{1 \over 2}(x-y))
développer.
On pose donc
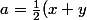)
et
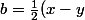)
on développe grâce aux formules de Simpson:
> sin(a)cos(b))
(1-cos(b)) >0)
>0)
d'où
il existe
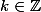
tel que
 \pi)
il s'agit donc de bandes dans la direction
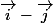
comme l'a écrit Ericovitchi (au fait, bonjour :we: )
sauf la 1ère diagonale du repère d'équation x-y=0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
