Bonjour,
Je me pose une question et je ne trouve pas la réponse. Une histoire de topologie engendrée.

est un ensemble non vide et
)
est un ensemble de parties de

. La topologie engendrée par

est la plus petite topologie sur

contenant

, c'est aussi l'intersection de toutes les topologies de

contenant

. On la note
)
On peut l'obtenir comme ceci : (on parle de fermeture par intersection finie et de fermeture par union quelconque)
Soit

l'ensemble des intersections finies d'éléments de

.

est alors une base de topologie de
)
et
)
est l'ensemble des unions quelconques d'éléments de

.
Ma question est la suivante : que se passe-t-il si on inverse les deux opérateurs de fermetures ? Si l'on pose :
Soit
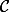
l'ensemble des unions quelconques d'éléments de

soit
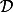
l'ensemble des intersections finies d'éléments de
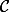
.
Mon intuition me dit que
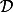
et
)
ne sont pas égaux. Et qu'on doit donc trouver un exemple où ces deux ensembles ne sont pas égaux (dans la droite réelle par exemple). Il est même possible que l'un des deux soit inclus dans l'autre. En fait je n'en ai pas grande idée...
Si quelqu'un a envie de se pencher un peu sur la question... Je suis très curieux !
Merci d'avance


