Une simple extension d'une conjecture simple

[CAMI]

Une conjecture bien connue est la suivante, soit x(1) un entier positif non nul premier nombre d'une suite , on applique les règles suivantes: si x(i) modulo 2 = 0 alors x(i+1) = x(i)/2, si x(i) modulo 2 = 1 alors
x(i+1) = 3*x(i)+1, quelque soit le nombre initial x(1) on finira toujours par aboutir après un certain nombre d'applications de la règle définie à tomber sur x(j) = 1 et x(j+1) = 4, x(j+2) = 2 , x(j+3) = 1 et perpétuelle répétition du cycle dit trivial 4, 2, 1.
Je décrit ici une nouvelle conjecture qui j'espère aura autant de succès que celle qui précède émise en 1937 juste l'année avant ma naissance et dont je pense avoir apporter la preuve mais sans pouvoir être compris, l'argument massif étant que si des milliers (pourquoi pas des millions) de mathématiciens se sont intéressés au sujet et n'ont pas trouvé de solution, ce n'est pas un simple Ingénieur comme moi qui peut prétendre apporter la preuve!
Voila la nouvelle conjecture ouverte le 17 août 2018 par Pierre CAMI, Ingénieur ESCIL promo 1961:
Soit Q un nombre premier, x(1) un nombre entier positif non nul numéro 1 de la suite, on applique les règles suivantes: si x(i) modulo 2 = 0 alors x(i+1) = x(i)/2, si x(i) modulo 2 = 1 et si x(i) est un nombre premier alors
x(i+1) = Q*x(i)+1, si x(i) est composite (donc non premier) x(i) = 3*x(i+1)+1.
Les matheux aurons tout de suite compris que si Q = 3 premier nombre premier impair on retombe sur la conjecture déjà bien connue, mais que ce passe t-il si Q premier est différent de 3?
Ma conjecture est la suivante, toutes les suites ainsi définies vont continuer pour une partie à se terminer par 1,4,2,1... quelque soit Q, toutes celles qui ne se terminent pas par 1 se terminent par un cycle commençant par un nombre premier R qui va se répéter éternellement après un certain nombre d'itérations. Pour un même nombre premier Q peuvent exister un seul nombre R ou plusieurs R1, R2, R3 premiers et plus. Quelque soit le nombre premier Q les suites convergent toujours vers 1 ou un cycle commençant par un nombre premier.
Un exemple avec Q = 2, pour x(1) impair < 61 on atteint le cycle trivial 1, 4, 2, 1.
Pour x(1) = 61 on atteint après 889 itérations le nombre premier R = 1163 et on retrouve 1163 après 930 itérations, de même pour x(1) = 81, 123, 139, 185, ....., 19977 est une infinité d'autres.
Pour ceux qui sont intéressés j'ai vérifié la conjecture et donc au moins trouvé les nombres premiers R pour tout premier Q jusqu'à 421 et x(1) jusqu'à 9999 pour les plus grands nombres premiers Q.
Compte tenu du nombre de réponses reçues après ma première tentative je suis prés à tout lire sauf les dénégations non argumentées ou infondées, par contre si il y a vraiment dés matheux ici je suis disposé à entendre toute critique argumentée et tenter d'apporter les réponses aux questions pertinentes.

[aviateur]

Bonjour
Il y a un problème, il faudrait revoir ton texte car si tu travailles sur (voire )

x(i+1) = 3*x(i+1)+1.

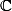un tel nombre n'existe pas.

l'argument massif étant que si des milliers (pourquoi pas des millions) de mathématiciens se sont intéressés au sujet et n'ont pas trouvé de solution, ce n'est pas un simple Ingénieur comme moi qui peut prétendre apporter la preuve!

D'autre part l'argument que nous avons apporté c'est que tu n'as pas fait de démonstration du tout.

[pascal16]

Un+1 = Un/2 si Un pair et Un+1 = 3Un + 1 si Un impair, ça me rappelle un autre post...

[CAMI]

Merci pour avoir vu la faute de frappe, j'ai pas ma vue de 20 ans hélas!.
En ce qui concerne la preuve ce qui me surprend le plus c'est que personne ne veut la voir ou essayer de la comprendre!
Je vais procéder par étape, si une des affirmation est erronée il faut me dire laquelle et le prouver, on parle bien entendu de la conjecture de Syracuse et des suites de Collatz, je défini ainsi les termes nécessaires à la démonstration:
un successeur est x(i+1) qui vient après x(i) dans une suite en ne considérant que les nombres impairs,
un prédécesseur est x(i) qui a précédé x(i+1) dans une suite en ne considérant que les nombres impairs.
1- Tout nombre impair prédécesseur de (6*n-5) est de la forme ((6*n-5)*2^(2*k)-1))3, n de 1 à N, k de 1 à K soit une infinité de prédécesseurs possibles .
2- Tout nombre impair prédécesseur de (6*n-1) est de la forme ((6*n-1)*2^(2*k-1)-1)3, n de 1 à N, k de 1 à K soit une infinité de prédécesseurs possibles .
3- Tout nombre impair (6*n-3) n'a aucun prédécesseur impair possible.
Tout nombre impair est représenté par soit ((6*n-5)*2^(2*k)-1))3, soit par ((6*n-5)*2^(2*k)-1))3 pour un couple n, k donné et tout les nombres impairs sont donc représenté une fois et une fois seulement (je crois que le langage des maths modernes utilise "est représenté de façon univoque par un couple n, k", je m'excuse d'être encore de la vieille école)
4- Chaque nombre impair 6*n-5 ou 6*n-1 a un successeur unique.
5- Si je défini une suite commençant par x(i) = 1 le premier prédécesseur de x(i) est x(i-1) = (2^(2*k)-1)/3 pour k>1 et k modulo 3 = 1 ou 2, mais jamais k modulo 3 =0 car la suite n'aura plus de prédécesseur impair, et k de 2 à K. Le 2ème prédécesseur x(i-2) sera soit (x(i-1)*2^(2*k)-1)/3 ou (x(i-1)*2^(2*k-1)-1)/3 non multiple de 3 pour continuer la suite et k de 1 à K, le 3ème prédécesseur x(i-3) sera soit (x(i-2)*2^(2*k)-1)/3 ou (x(i-2)*2^(2*k-1)-1)/3 non multiple de 3 pour continuer la suite et k de 1 à K, ..............
le nième prédécesseur x(i-n) sera soit (x(i-n+1)*2^(2*k)-1)/3 ou (x(i-n+1)*2^(2*k-1)-1)/3 non multiple de 3 pour continuer la suite et k de 1 à K et ainsi de suite.
Cette suite inverse ne peut que diverger plus ou moins lentement suivant les valeurs de k à chaque étape et ce qui est remarquable c'est que chaque valeur impaire multiple de 3 peut être obtenue.
La prochaine étape à plus tard (peut être ?)

[aviateur]

Moi j'abandonne .
Si ça te fait plaisir alors je vais dire ce que tu veux entendre. Une armée de mathématiciens ne sait pas démontrer la conjecture de Collatz alors ce n'est pas un quelconque ingénieur à la retraite qui savoir démontrer la conjecture.
Je sais que cela va en faire rire quelques uns.
L'aviateur ne s'est pas écrasé, il va voler vers d'autres cieux.

[CAMI]

Je ne sais pas qui vous êtes, vous semblez régner ici comme un seigneur, je me suis présenté, Pierre CAMI ingénieur ESCIL promotion 1961, sur l'annuaire (ex PTT).
Juste une question qui êtes vous ?

[pascal16]

On peut toujours progresser, il y a d'autre problèmes du millénaire.

Perso j'ai appris il y a deux jours la force de la transformée LU de matrices alors que ça fait des années que j'avais pigé que le pivot de Gauss séparé en une descente et une remontée avait un intérêt énorme mal exploité.

[aviateur]

Par correction il serait bien de faire tes critiques par message privé pour le bien du forum. Mais je réponds une dernière fois et définitivement:
D'abord, je n'ai pas à décliner mon identité. Disons, qu'ici sur ce forum, je suis présent pour aider autant que possible les personnes qui demandent de l'aide en mathématiques (et à coup sûr je ne pense pas être le seul et heureusement).
Mais avant tout, l'important pour moi c'est la promotion des mathématiques. Vraiment, si par notre aide on arrive à aider un jeune lycéen ou étudiant à mieux comprendre et parler des mathématiques alors c'est gagné.
La contrepartie d'un tel forum c'est qu'ici qu'on ne peut pas laisser passer des posts où il y a n'importe quoi. J'espère que tu comprends où je veux en venir.
D'autre part je ne règne pas en seigneur mais simplement mes interventions sont plus fréquentes en ce moment car je suis assez libre. Mais ne t'inquiètes pas, il y a d'autres seigneurs ici.

[nodgim]

Il me semble que, pour cette seconde conjecture ou pour l'originale, présentée l'une et l'autre par CAMI, l'auteur verse dans les 2 cas dans les mêmes errements, qu'on lui a déjà montrés plus d'une fois, mais qu'il s'obstine à ignorer : ce n'est pas parce que la remontée des suites donne une infinité de nombres que pour autant on obtient TOUS les nombres. Pour être sûr d'avoir bien tous les nombres, il faut le démontrer d'une façon ou d'une autre, ce qui n'est pas fait.

CAMI s'interroge sur le niveau général des intervenants ici, c'est très divers, du simple bachelier (dont je) au professeur d'école préparatoire. Mais il n'y a pas ici besoin d'être bardé de médailles pour s'apercevoir de l'inanité du développement exposé (on est bien loin de la rigueur d'une démonstration, même incomplète, pour mériter ce mot).

Qu'on se plante, ça arrive à tout le monde et tous les jours. Mais qu'on persiste dans le déni des critiques faites, c'est plus embêtant.

[nodgim]

Sinon, CAMI, si tu t'estimes injustement rejeté sur ce site, tu peux par exemple aller à cette adresse :
www.forum.math.ulg.ac.be, site de math géré par l'université de Liège, et y exposer tes idées. Il est hanté par des profs d'université, qui te donneront volontiers leur avis.

[Ben314]

Salut,

Je décrit ici une nouvelle conjecture qui j'espère aura autant de succès que celle qui précède émise en 1937 juste l'année avant ma naissance et dont je pense avoir apporter la preuve mais sans pouvoir être compris, l'argument massif étant que si des milliers (pourquoi pas des millions) de mathématiciens se sont intéressés au sujet et n'ont pas trouvé de solution, ce n'est pas un simple Ingénieur comme moi qui peut prétendre apporter la preuve!

Ca m’intéresserait bien d'avoir (ne serait-ce qu'une vague) idée de la preuve si ce n'est pas indiscret.
Si tu parle de ce que tu as écrit dans l'autre fils, alors :
- Je n'y vois nulle part une quelconque allusion au fait que ton truc est faux du fait que tu n'est pas mathématitien professionnel.
- Par contre j'y vois de multiple et grossières erreurs de raisonnement ainsi que de nombreuses affirmations purement gratuites (dont certaines trivialement fausses).

P.S. Et, comme à mon avis la grande majorité des lecteur de ton texte, je me suis arrêté à cette partie là de ta prose vu qu'elle signifie que tu ne tient nullement compte du fait qu'on t'a signalé (de grossières) erreurs de raisonnement dans le thread précédent ce qui signifie que le temps qu'on a passé à te lire a été totalement perdu.

[Pseuda]

Bonjour,

Pour ma part, je ne lis plus et je ne réponds plus ce qui vient de @CAMI (soit il ne voit toujours pas d'où vient son erreur, et c'est embêtant quand on veut "démontrer" la conjecture de Collatz, soit il la voit, et comme dit @nodgim, ne pas vouloir reconnaître ses erreurs est très désobligeant pour ses lecteurs). Bref, il veut se donner l'illusion qu'il a démontré la conjecture, si cela lui fait plaisir, grand bien lui fasse.

Sinon, sache @CAMI qu'on parle de toi, et de beaucoup d'autres, dans cet article que j'ai trouvé très intéressant, qui fait un état des lieux de ce que cette conjecture peut susciter en recherches par des mathématiciens amateurs et professionnels, en conjectures non démontrées, etc... :

https://hal.archives-ouvertes.fr/hal-01593181/document