Une inclusion modulo

[tournesol]

Bonne année à tous et bonne motivation à tous les étudiants.
J'ai remarqué, grâce à ma casio graph 35 , que pour tout entier naturel non nul n , les représentants des puissances de 10 modulo 3^n compris entre 1 et 3^n-1 sont tous des représentants de puissances de 10 modulo 3^(n+1) . Je n'ai pas réussi à le démontrer .

[tournesol]

Il semblerait que l'on puisse remplacer 10 par n'importe quel entier premier ave 3 .

[tournesol]

je relance ma conjecture en la formulant dans toute sa généralité .
Soit p un nombre premier et a un entier naturel premier avec p .
Pour tout entier naturel non nul n , je note Rn l'ensemble des restes de la division euclidienne des puissances de a par p^n . La conjecture est : la suite (Rn) est croissante pour l'inclusion des ensembles .
Si quelqu'un peut me fournir des indications pour la démontrer , je le remercie par avance .

[Ben314]

Salut,
Je suis pas sûr d'avoir bien compris : si p=5 et a=7, c'est quoi l'ensemble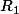 ? et ?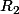
Remarque : dans cas, a est d'ordre 4 modulo p et il est aussi d'ordre 4 modulo p²