Trouver un supplémentaire
18 messages
- Page 1 sur 1
Trouver un supplémentaire
Bonjour à tous,
E désigne l'espace vectoriel des applications de R dans R de classe C2.
F désigne le SEV des polynômes de degré au plus égal à 2.
Il s'agit de déterminer un supplémentaire de F dans E.
Des considérations sur les dimensions me viennent à l'esprit... Quelqu'un a-t-il une piste ?
Merci !
E désigne l'espace vectoriel des applications de R dans R de classe C2.
F désigne le SEV des polynômes de degré au plus égal à 2.
Il s'agit de déterminer un supplémentaire de F dans E.
Des considérations sur les dimensions me viennent à l'esprit... Quelqu'un a-t-il une piste ?
Merci !
Re: Trouver un supplémentaire
Salut,
Perso, ce qui me vient à l'esprit, c'est qu'il faut écrire toute fonction f C2 sur [0,1] sous la forme unique f=P+g où P est un polynôme de degré au plus 2 et où g est une fonction . . . ayant une certaine propriété . . .
Et ce que ça évoque pour moi, c'est par exemple les développements limités : on pourrait prendre pour P le D.L. à l'ordre 2 (en 0 par exemple) de f. Quelle propriété pourrait alors caractériser les restes g=f-P ?
C'est cette propriété là que tu peut prendre comme définition de ton s.e.v. G.
Sinon, le truc dont il faut bien être conscient c'est que des supplémentaires, il y en a des tonnes (une GROSSE infinité) donc ce que je te propose là, c'est une méthode pour en trouver UN parmi d'autre.
Un autre type de raisonnement (avec la notion de codimension et celle de forme linéaire) pourrait conduire à prendre comme supplémentaire l'ensemble des fonction f qui sont nulle en 0, en 1/2 et en 1 (ou qui prennent n'importe quelle valeurs fixées d'avance en 3 points distincts fixés de [0,1]). Est ce que tu voit pourquoi ça marche ? (ou au pire est-ce que tu arive à montrer que c'est bien un supplémentaire de ton e.v.)
Déjà, a, a risque pas de te mener à grand chose vu que l'espace des fonctions C2 sur [0,1] est clairement de dimension infini (il contient au moins tout les polynômes . . . )jeje56 a écrit:Des considérations sur les dimensions me viennent à l'esprit... Quelqu'un a-t-il une piste ?
Perso, ce qui me vient à l'esprit, c'est qu'il faut écrire toute fonction f C2 sur [0,1] sous la forme unique f=P+g où P est un polynôme de degré au plus 2 et où g est une fonction . . . ayant une certaine propriété . . .
Et ce que ça évoque pour moi, c'est par exemple les développements limités : on pourrait prendre pour P le D.L. à l'ordre 2 (en 0 par exemple) de f. Quelle propriété pourrait alors caractériser les restes g=f-P ?
C'est cette propriété là que tu peut prendre comme définition de ton s.e.v. G.
Sinon, le truc dont il faut bien être conscient c'est que des supplémentaires, il y en a des tonnes (une GROSSE infinité) donc ce que je te propose là, c'est une méthode pour en trouver UN parmi d'autre.
Un autre type de raisonnement (avec la notion de codimension et celle de forme linéaire) pourrait conduire à prendre comme supplémentaire l'ensemble des fonction f qui sont nulle en 0, en 1/2 et en 1 (ou qui prennent n'importe quelle valeurs fixées d'avance en 3 points distincts fixés de [0,1]). Est ce que tu voit pourquoi ça marche ? (ou au pire est-ce que tu arive à montrer que c'est bien un supplémentaire de ton e.v.)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trouver un supplémentaire
Ben314 a écrit: on pourrait prendre pour P le D.L. à l'ordre 2 (en 0 par exemple) de f. Quelle propriété pourrait alors caractériser les restes g=f-P ?
Salut Ben, merci de ta réponse.
g serait telle que
Mais je n'arrive pas à concevoir la décomposition de toute fonction f en une telle somme directe pour tout x puisque le DL est local...
Merci de ton aide.
Re: Trouver un supplémentaire
Bonjour,
Mais la différence entre la fonction de classe sur
sur  et la partie régulière de son développement limité en 0 d'ordre 2 est bien une fonction de classe
et la partie régulière de son développement limité en 0 d'ordre 2 est bien une fonction de classe  sur
sur  .
.
Mais la différence entre la fonction de classe
Re: Trouver un supplémentaire
GaBuZoMeu a écrit:Bonjour,
Mais la différence entre la fonction de classesur
et la partie régulière de son développement limité en 0 d'ordre 2 est bien une fonction de classe
sur
.
Oui... Ce qui me gêne est qu'une telle décomposition f=P+g est vraie seulement au voisinage de 0, non ?
Re: Trouver un supplémentaire
C'était une réponse à
Ce que je veux dire est donc que cette décomposition est bien une décomposition dans) , et que "vraie seulement au voisinage de 0" ne fait pas sens.
, et que "vraie seulement au voisinage de 0" ne fait pas sens.
une telle décomposition f=P+g est vraie seulement au voisinage de 0
Ce que je veux dire est donc que cette décomposition est bien une décomposition dans
Re: Trouver un supplémentaire
Oui d'accord, j'y vois plus clair.
Une rédaction par analyse synthèse est-elle appropriée ici ?
Merci !
Une rédaction par analyse synthèse est-elle appropriée ici ?
Merci !
Re: Trouver un supplémentaire
Ça peut se faire. Mais il faut commencer par bien identifier le candidat supplémentaire (et vérifier que c'est bien un sous-espace vectoriel).
Re: Trouver un supplémentaire
Je propose la rédaction suivante.
Soit)
Par unicité du développement limité d'ordre n d'une fonction en un point, il existe un unique polynôme et une unique fonction
et une unique fonction ) vérifiant
vérifiant } {x^2} = 0) tels que
tels que 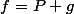 .
.
Reste à vérifier que/\lim_{x\rightarrow 0} \frac {g(x)} {x^2} = 0\}) est bien un sous-espace vectoriel de
est bien un sous-espace vectoriel de ) :
:
- contient
contient  donc est non vide ;
donc est non vide ;
-(x)} {x^2}=\lim_{x\rightarrow 0} \frac {f(x)} {x^2} +\lambda \lim_{x\rightarrow 0} \frac {g(x)} {x^2} = 0) .
.
En conclusion, est bien un supplémentaire de
est bien un supplémentaire de 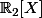 dans
dans ) .
.
Est-ce correct ?
Merci d'avance !
Soit
Par unicité du développement limité d'ordre n d'une fonction en un point, il existe un unique polynôme
Reste à vérifier que
-
-
En conclusion,
Est-ce correct ?
Merci d'avance !
Re: Trouver un supplémentaire
Ça marche.
Tu aurais pu aussi caractériser ton supplémentaire comme le sous-espace des g\in C^2(\R) tels que g(0)=g'(0)=g''(0)=0.
Et pour montrer qu'il n'est pas vide : il y a 0 (la fonction contante nulle) dedans.
Comme l'a suggéré Ben,, tu aurais pu prendre le sous-espace des) tels que
tels que =g(1)=g(2)=0) , ou le sous-espace des
, ou le sous-espace des ) tels que
tels que =g'(0)=0) et
et \,\mathrm dt=0) ou ...
ou ...
Tu aurais pu aussi caractériser ton supplémentaire comme le sous-espace des g\in C^2(\R) tels que g(0)=g'(0)=g''(0)=0.
Et pour montrer qu'il n'est pas vide : il y a 0 (la fonction contante nulle) dedans.
Comme l'a suggéré Ben,, tu aurais pu prendre le sous-espace des
Re: Trouver un supplémentaire
GaBuZoMeu a écrit:Ça marche.
Tu aurais pu aussi caractériser ton supplémentaire comme le sous-espace des g\in C^2(\R) tels que g(0)=g'(0)=g''(0)=0.
Je ne vois pas... S'agit-il du même G que moi caractérisé différemment ?
Re: Trouver un supplémentaire
Réfléchis. Que veut dire =o(x^2)) au voisinage de 0, pour une fonction de classe
au voisinage de 0, pour une fonction de classe  ?
?
Re: Trouver un supplémentaire
Je ne vois toujours pas le lien entre le statut de négligeable devant  et g(0), g'(0) et g''(0)...
et g(0), g'(0) et g''(0)...
Re: Trouver un supplémentaire
Veux-tu me faire croire que tu n'as jamais entendu parler de la formule de Taylor-Young ?
Re: Trouver un supplémentaire
on peut choisir aussi le polynôme interpolateur de Lagrange en 3 points (unicité du polynôme si je ne trompe pas) pour la décomposition unique.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
