Trouver la réciproque d'une fonction
19 messages
- Page 1 sur 1
trouver la réciproque d'une fonction
salut, j'aurais besoin d'aide pour trouver la réciproque d'une fonction.
f(x)=x/(1+valeur absolue de x)
le prob c'est que j'ai pas compris comment on trouve la réciproque d'une fonction.
est ce que quelqu'un peu m'aider?
f(x)=x/(1+valeur absolue de x)
le prob c'est que j'ai pas compris comment on trouve la réciproque d'une fonction.
est ce que quelqu'un peu m'aider?
Mag a écrit:ok mais cela revient à démontrer qu'elle est surjective non?
oui, s'il y a des solutions .
Et s'il a au maximum une solution, cela montre qu'elle est injective !
Mais si tu veux la fonction réciproque, c'est que la fonction est bijective (injective et surjective), non ? En résolvant cette équation, tu prouveras d'un seul coup que la fonction est bijective et tu trouveras sa fonction réciproque : tout bénef ! :id:
Mag a écrit:Donc si j'ai démontrée qu'elle est injective et surjective, j'ai aussi trouvée la réciproque par la même occasion?
Tout dépend de la méthode employée ! Il y a des méthodes abstraite qui justifient que la fonction est bijective sans donner explicitement la réciproque.
Au fait, comment as-tu démontré que la fonction est surjective ?
Un tableau de variation permet de prouver qu'une fonction est (ou n'est pas) injective, surjective, bijective, mais ne donnera jamais la fonction réciproque d'une fonction bijective.
Bref, ici, comme les calculs sont simples, résoudre en x l'équation f(x)=y permet de tout faire d'un coup : c'est <> plus efficace !
Bref, ici, comme les calculs sont simples, résoudre en x l'équation f(x)=y permet de tout faire d'un coup : c'est <
j'ai résolu f(x)=y, pour x<0 et x>0 et je trouve donc deux solutions: x=y/1-y et x=y/1+y
dc comme il ya deux solution on a bien une surjection
comme j'ai déjà montré l'injection, je sais que la fonction est bijective
maintenant je cherche sa réciproque. Je dois utiliser f(x)=y d'après ce que tu m'a di mais quelle solution de cette équation?
dc comme il ya deux solution on a bien une surjection
comme j'ai déjà montré l'injection, je sais que la fonction est bijective
maintenant je cherche sa réciproque. Je dois utiliser f(x)=y d'après ce que tu m'a di mais quelle solution de cette équation?
Précisément
x=y/(1-y) quand

x=y/(1+y) quand

non, il n'y a pas 2 solutions (sinon la fonction ne serait pas injective par exemple !).
Pour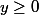 , tu prends
, tu prends =y/(1-y))
Pour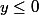 , tu prends
, tu prends =y/(1+y))
Autrement dit, pour y quelconque=y/(1-|y|))
Au fait, la fonction est une bijection de quoi sur quoi ?
x=y/(1-y) quand
x=y/(1+y) quand
Mag a écrit:dc comme il ya deux solution on a bien une surjection
non, il n'y a pas 2 solutions (sinon la fonction ne serait pas injective par exemple !).
Pour
Pour
Autrement dit, pour y quelconque
Au fait, la fonction est une bijection de quoi sur quoi ?
oui oui je suis ok j'avais effectivemen toubliée de prendre en compte que -y et +y pouvaient s'arranger en prenant la valeur absolue.
En tout cas merci pour ton aide
Je vais essayer de faire le reste de mon DM mais si je n'y arrive pas tant pis, au moins j'aurais compris cet exo.
je te ferais savoir si c'est juste (ce dont je ne doute pas) quand on aurra corrigé
Encore merci pour ton aid eprécieuse
En tout cas merci pour ton aide
Je vais essayer de faire le reste de mon DM mais si je n'y arrive pas tant pis, au moins j'aurais compris cet exo.
je te ferais savoir si c'est juste (ce dont je ne doute pas) quand on aurra corrigé
Encore merci pour ton aid eprécieuse
Remerciement
boujour à tous
bon voilà je fais suite à ce message pour remercier léon1789 de m'avoir autant aidé de weekend, sachant que tout ce qu'il m'avait suggéré était correct.
Donc Merci beaucoup
bon voilà je fais suite à ce message pour remercier léon1789 de m'avoir autant aidé de weekend, sachant que tout ce qu'il m'avait suggéré était correct.
Donc Merci beaucoup
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
