Trouver une fonction réciproque
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 02:40
par shigeno » 15 Déc 2007, 02:40
Bonjour j'aimerais savoir s'il y a une méthode particulière pour trouver une fonction réciproque ou si c'est du cas par cas ? Parce que là j'ai une fonction, de N² dans N et on demande de trouver sans calculs une réciproque donc voila, merci pour votre réponse.
-
Noemi
- Membre Complexe
- Messages: 3241
- Enregistré le: 20 Oct 2007, 16:09
-
 par Noemi » 15 Déc 2007, 10:37
par Noemi » 15 Déc 2007, 10:37
Une méthode :
Vérifiez que la fonction est bijective.
Inversez le couple (x;y)
isolez y en fonction de x.
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 11:09
par shigeno » 15 Déc 2007, 11:09
Inverser le couple (x,y) ? C'est-à-dire ?
Et pourquoi isoler y en fonction de x, puisqu'on a une valeur z en fonction de x et y, il ne faudrait pas plutôt avoir x et y en fonction de z ?
-
Noemi
- Membre Complexe
- Messages: 3241
- Enregistré le: 20 Oct 2007, 16:09
-
 par Noemi » 15 Déc 2007, 11:37
par Noemi » 15 Déc 2007, 11:37
Vu que je n'avais pas la fonction, j'ai choisi le cas le plus simple f(x) = y.
Pour un cas plus compliqué, il faut éventuellement utiliser les matrices jacobiennes.
Indique ta fonction.
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 11:46
par shigeno » 15 Déc 2007, 11:46
Matrices jacobiennes ?? oula :)
La fonction est z = 1/2 (x+y)(x+y+1)+x.
J'avoue que j'ai du mal à trouver sa réciproque.
-
melreg
- Membre Relatif
- Messages: 325
- Enregistré le: 10 Déc 2007, 20:09
-
 par melreg » 15 Déc 2007, 11:50
par melreg » 15 Déc 2007, 11:50
Bonjour,
La fonction est z = 1/2 (x+y)(x+y+1)+x
Donc l'image de (0,0) est z=0 et celle de (0,-1) est aussi z=0.
Il y aura un petit problème pour inverser...non?
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 11:52
par shigeno » 15 Déc 2007, 11:52
ouais j'ai oublié de dire que ça allait de N² dans N donc pas d'entiers négatifs :)
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 15 Déc 2007, 12:52
par alben » 15 Déc 2007, 12:52
Bonjour,
Pour trouver sans calcul, il te faut faire un tableau avec x en colonne, y en ligne et voir à quoi ressemblent les valeurs de z...
Sinon, avec calcul, pose u=x+y comme x ne peut être plus grand que u, on trouve facilement que
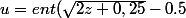)
et
}{2}\; y=u-x)
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 13:05
par shigeno » 15 Déc 2007, 13:05
Merci pour la version avec calcul.
Mais pour la version sans, c'est ce que j'ai fait, je vois les valeurs en diagonale, mais pour trouver une relation... dur dur.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 15 Déc 2007, 13:37
par ThSQ » 15 Déc 2007, 13:37
Un version
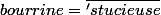
:
Tu résouts en y, tu trouves une racine carrée avec du z et du x qui doit être un carré. Tu reportes pour avoir y.
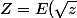)
(E = partie entière)
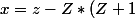/2)
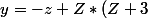/2)
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 14:50
par shigeno » 15 Déc 2007, 14:50
Tu es sûr du résultat ? Parce que quand je calcule je n'obtiens pas les bonnes valeurs.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 15 Déc 2007, 16:04
par ThSQ » 15 Déc 2007, 16:04
shigeno a écrit:Tu es sûr du résultat ? Parce que quand je calcule je n'obtiens pas les bonnes valeurs.
Ben oui je viens de vérifier.
-
shigeno
- Membre Naturel
- Messages: 10
- Enregistré le: 07 Déc 2007, 15:34
-
 par shigeno » 15 Déc 2007, 16:09
par shigeno » 15 Déc 2007, 16:09
Ah oui, j'ai calculé en inversant x et y, oui effectivement c'est bien ça, merci.
 par busard_des_roseaux » 16 Déc 2007, 16:15
par busard_des_roseaux » 16 Déc 2007, 16:15
ThSQ a écrit:Un version
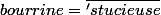
:
Tu résouts en y, tu trouves une racine carrée avec du z et du x qui doit être un carré. Tu reportes pour avoir y.
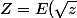)
(E = partie entière)
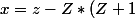/2)
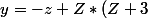/2)
bonjour ThSQ,
ça a l'air faux :doh:
z=f(1,2)=7
Z=2
x=4
y= -2
????
par contre, je trouve le même résultat qu'Alben.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
