Bonjour,
Équation de base:
T(w) = -jwk/(1-j(w/2)) k étant un nombre réel strictement positif
Je n'arrive pas à voir comment prouver que l'argument du nombre complexe
(-jwk)^3 est égal a PI/2
Pour le suivant je l'aurais trouvé mais je vois pas comment le prouver, j'aurais utilisé directement la formule que l'on m'a donner.
a-jb -> -arctan (b/a)
Pour l'exemple dans le précèdent examen que je révise c'est noté:
1-j(w/2) l'argument est -arctan(w/2)
Merci de votre aide, Examen demain après midi, c'est pas facile de si remettre et la mémoire flanche...
Trouver l'argument
6 messages
- Page 1 sur 1
pour un nombre complexe (non nul) écrit sous la forme algébrique a+jb , il est possible de calculer son module et son argument de la manière suivante :
module :
Soit un argument du nombre complexe a+jb . Alors on a :
un argument du nombre complexe a+jb . Alors on a :
 = \frac{a}{\sqrt{a^2 + b^2}})
 = \frac{b}{\sqrt{a^2 + b^2}})
donc = \frac{sin(\theta) }{cos(\theta)} =\frac{b}{a})
donc, argument :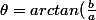)
On procède de la même manière pour un nombre complexe écrit sous la forme a-jb (qui est le nombre complexe conjugué de a+jb)...mais il faut faire attention au signe "moins" : un argument de a-jb est = - arctan(\frac{b}{a})) , car la fonction arctangente est impaire ! Tu retrouves ainsi le fait que 1-j(w/2) a pour argument arctan(-(w/2) / 1 ) = arctan( -(w/2) ) = - arctan(w/2)
, car la fonction arctangente est impaire ! Tu retrouves ainsi le fait que 1-j(w/2) a pour argument arctan(-(w/2) / 1 ) = arctan( -(w/2) ) = - arctan(w/2)
module :
Soit
donc
donc, argument :
On procède de la même manière pour un nombre complexe écrit sous la forme a-jb (qui est le nombre complexe conjugué de a+jb)...mais il faut faire attention au signe "moins" : un argument de a-jb est
Attention, ceci n'est valable QUE pour a > 0.MacManus a écrit:pour un nombre complexe (non nul) écrit sous la forme algébrique a+jb , il est possible de calculer son module et son argument de la manière suivante :
module :
Soitun argument du nombre complexe a+jb . Alors on a :
 = \frac{a}{\sqrt{a^2 + b^2}})
 = \frac{b}{\sqrt{a^2 + b^2}})
donc = \frac{sin(\theta) }{cos(\theta)} =\frac{b}{a})
donc, argument :
Pour a < 0, cela devient
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
